I built this as a test project to explore the forefront of LLM tools and opportunities in public health. The AI COVID + Flu Analyst app is a tool designed for today’s healthcare challenges. Developed using Streamlit, this app not only taps into millions of news sources and up-to-the-minute CDC data but also incorporates an LLM RAG (Retrieval-Augmented Generation) architecture, showcasing our commitment to advancing AI applications in meaningful ways. I built this project as a perfect platform to experiment with LLM RAG architectures, delve into LanChain operations, utilize the OpenAI API, and engage with Streamlit community cloud. Aimed at providing a robust monitoring dashboard, the app integrates several forecasting methods to track and analyze flu and COVID infections, setting a new standard in disease surveillance and response.

Check out the cloud hosted app here : Streamlit App

Features

1. Descriptive & Predictive Infection Dashboard

• Description: Displays the latest infection data in the US from the CDC, combined with Census geo-spatial data.
• Visualization: Maps infections by total number and rate.
• Forecasting: ARIMA models forecast infection numbers, offering insight into bulk numbers by state and region.

2. Interactive AI News Analyst

• Functionality: Uses an LLM RAG deployment to allow users to interactively query the latest news on COVID and hospitalizations in the US and globally.

3. Forecasted Hospital Burden

• Prediction: Forecasts the impact on each state’s hospital systems by predicting infections, hospitalization rates, and hospital capacity.
• Insights: Evaluates the burden of flu and COVID patients on hospital bed capacity and issues warnings for potential capacity concerns.

Quick Start Guide

Follow these steps to set up and run the app on your local machine.

Prerequisites

1. Install Git.
2. Create an account on the OpenAI Developer Platform.
3. Create a free account with News API.

Setup

1. Clone the Repository:

    git clone https://github.com/yourusername/yourproject.git
    cd yourproject
   

2. Update the API Keys:
   • Add your OpenAI API Key to oai_template.yaml and rename the file to oai.yaml.
   • Add your News API Key to newsapi_template.yaml and rename the file to newsapi.yaml.
3. Setup the Python Virtual Environment:

    venv/Scripts/Activate
   

4. Run the Streamlit App:

    streamlit run ./src/streamlit/app.py
   

Access the App

Once the server is running, open your browser and navigate to http://localhost:8182.

This section outlines the architecture and functionality of the implemented Retrieval-Augmented Generation (RAG) model, which integrates news data from NewsAPI, user query handling through Streamlit, and response generation using OpenAI’s API.

Workflow Description

1. Data Ingestion and Processing Source: News articles are fetched from NewsAPI. Embedding: Articles are converted into vector representations using FAISS (Facebook AI Similarity Search) embeddings, which capture the semantic content of the articles for effective retrieval.
2. Vector Database Storage Storage: The embeddings are stored in a Vector Database optimized for fast and accurate similarity searches.
3. User Query Interface Interface: Users input queries via a Streamlit-based interface, designed for simplicity and ease of use.
4. Document Retrieval Retrieval: Upon receiving a user query, the system retrieves the most relevant documents from the Vector Database using the semantic similarity of their embeddings to the query.
5. Integration with OpenAI Models Contextualization: The retrieved documents provide context to the OpenAI model, enhancing its ability to generate relevant and informed responses.
6. Response Generation Output: The system generates responses that are augmented with information directly cited from the retrieved documents, ensuring that responses are both relevant and grounded in sourced data. System Benefits Accuracy: Combines the computational efficiency of FAISS embeddings with the linguistic prowess of OpenAI models. Relevance: Ensures responses are contextually relevant by using document retrieval as a basis for response generation. Efficiency: Provides quick and reliable access to information through an optimized vector database.

This section provides an overview of the data engineering techniques employed in the system to fetch and process real-time news stories from NewsAPI and epidemiological data from the CDC via the Delphi Epidata API.

News Data Retrieval

The system dynamically retrieves current news stories from NewsAPI, which are then processed to serve as the foundation for generating insights:

• API Integration : News stories are fetched in real-time using NewsAPI, ensuring the content is current and relevant.
• Data Handling : Stories are parsed and necessary attributes like headlines, content, and publication dates are extracted and stored for further processing.

COVID Data Acquisition

We obtain real-time epidemiological data directly from the CDC through the Delphi Epidata API. This process is detailed in the following steps:

• API Usage : The system makes requests to the Delphi Epidata API to fetch the latest available data on flu and COVID-like illness surveillance.
• Date Range Handling : Data for specific epidemiological weeks (epiweeks) is requested, with the system calculating the range based on the current date to ensure the most recent data is retrieved.
• Data Transformation : Retrieved data is transformed into a structured format, making it suitable for analysis and integration into the system’s data pipeline.

Data Storage and Access

Data fetched from both NewsAPI and the CDC is stored locally to facilitate quick access and processing:

• Temporary Storage : News articles and COVID data are initially stored in a temporary directory, which is periodically cleaned to ensure data freshness and relevance.
• Reference Data Management : Static reference data, such as state population statistics, is stored separately and utilized to enrich the COVID data with demographic insights.

On-Demand Data Refresh

To manage computational resources efficiently and avoid unnecessary data fetches, the system employs an on-demand data refresh strategy:

• Streamlit Interface : Users can trigger data updates directly from the Streamlit interface via a ‘Refresh Data’ button. This ensures that the dashboard displays the most current information without the need for continuous background processing.
• Session State Management : Upon refreshing, the new data is loaded and saved to Streamlit’s session state. This approach ensures that the updated state is retained across app refreshes and during the user session, enhancing the user experience by providing continuity and speed in data interaction.

Automated Data Processing

Once new data is fetched, it is processed automatically to update the system’s insights:

• Data Preprocessing : New data goes through a cleaning and preprocessing pipeline to match the system’s requirements for analysis.
• Information Retrieval Setup : For the RAG system, news data is embedded using machine learning models and stored in a vector database for quick retrieval based on semantic similarity to user queries.

Conclusion

Our data engineering practices are designed to ensure that the system remains responsive and current, providing users with reliable and up-to-date information. The integration of on-demand refresh capabilities with robust data processing pipelines allows for efficient resource usage while maintaining high data quality and system performance.

Demystifying Data in Semiconductor Manufacturing with Fabscape

In the intricate and ever-evolving world of semiconductor manufacturing, the ability to seamlessly collect, analyze, and visualize data is more crucial than ever. Fabscape, an open platform designed for the semiconductor industry, stands out by offering these capabilities in a customizable and collaborative environment. My experience with Fabscape, shared during a live demo with Semiconductor Digest in March 2023, highlights the platform’s utility and my role in enhancing its data capabilities.

The Genesis of Our Fabscape Demo

Alongside Yuji Minegishi from Gigaphoton, I demonstrated how semiconductor developers could transform a blank slate into a dynamic data visualization tool using Fabscape. This platform isn’t just another software suite; it’s a robust foundation for innovation in data management within the semiconductor sector.

Building Blocks of Fabscape

Fabscape is built on a modular structure that supports extensive customization through plugins and drivers. These components are essential for tailoring the platform to meet the specific needs of device manufacturers and equipment vendors:

• Plugins: These add functionalities to Fabscape, allowing for specialized data visualization. Without plugins, Fabscape would be merely an empty shell.
• Drivers: These are crucial for data acquisition, tasked with collecting data directly from equipment and making it accessible to Fabscape’s backend. Like plugins, drivers are deployed as Docker containers, simplifying development and deployment and making individual services (including ML services) modular.

My Role in the Digital Transformation Department

As a member of the Digital Transformation Department at Gigaphoton, I contributed to enhancing the data capabilities of Fabscape, particularly in the realm of machine learning. I developed several key plugins for Gigaphoton equipment that enabled advanced ML model functionalities, aligning with the strict security, hardware, and communication standards of the semiconductor manufacturing environment. My focus was on designing plugins that facilitate the ingestion, storage, and processing of data, as well as serving sophisticated machine learning models. This included implementing architectures that support the seamless integration of these models into Fabscape, and setting up systems to monitor their performance and facilitate ongoing development.

From Data Collection to Predictive Analytics

During the demo, I created a driver to collect data—not from semiconductor equipment but from a public API providing COVID statistics. This example illustrated how Fabscape could be adapted for various data sources. We chose gRPC for the protocol to fetch data due to its high performance and efficiency in low-latency, high-throughput scenarios, which are crucial in semiconductor manufacturing environments. Additionally, gRPC’s strong type-safety, straightforward IDL (Interface Definition Language), and support for multiple programming environments make it an ideal choice for our scalable and interoperable system. I then integrated a user interface that leveraged reusable code components to display this data effectively.

Further extending Fabscape’s capabilities, I showcased how to integrate AI and machine learning for predictive analytics. Using a custom Jupyter Notebook plugin developed for Fabscape, we were able to pull equipment parameter data, apply machine learning models, and perform predictive analytics to forecast equipment behavior.

Why Fabscape?

Fabscape’s architecture promotes a collaborative approach, crucial for tackling complex challenges in semiconductor manufacturing. Its ability to be customized with proprietary and secure data solutions allows organizations to maintain data privacy while benefiting from shared innovations.

Engage with Fabscape

For those interested in exploring the potential of Fabscape, the platform offers a free Toolkit for developers. For more tailored solutions, Gigaphoton’s Advisory Program provides an opportunity to work directly with experts like myself to refine your data strategy and enhance your manufacturing processes.

Conclusion

The full capabilities of Fabscape were on display during the Semiconductor Digest webinar, which is available on demand. This event was not only a demonstration of technology but also a testament to the collaborative and innovative spirit that drives the semiconductor industry forward, and my role as a data scientist and engineer in shaping this future.

I invite you to watch the full recording to appreciate the depth of the solutions provided and to understand how Fabscape could revolutionize data management in your fab operations.

Being a good data scientist is more than being able to create an ad-hoc model on a curated data set. To bring true value with ML means planning and implementing the architecture to ingest, store, process data, serve the model, monitor, and facilitate ongoing development.

Working in the Digital Transformation Department of Gigaphoton, I contributed to a flexible open data platform to serve the strict security, hardware, and communication standards of the environment of the semiconductor Fab.

Abstract

XXX

Poster

PDF

Medication Regimen Complexity (MRC) may not be a term familiar to those outside of the medical field, yet in clinical circles, it plays an integral role in assessing a patient’s prescribed medications. MRC is a comprehensive evaluation that extends beyond merely tallying the number of medications. It delves into the specifics of each medication: the type, dosing frequency, and potential interactions. This deeper dive provides a holistic view of a patient’s health status and treatment trajectory. However, there is uncertainty as to the optimal metric, which translates to uncertainy in using these metrics for clinical decisions. It’s within this critical aspect of healthcare that I applied predictive classification models, aiming to unveil the predictive potential of MRC and its variants in determining patient outcomes.

Working alongside the clinical research experts Todd Brothers PhD, PharmD, and Mohammad Al-Mamun PhD, during my time at the Northeast Big Data and Innovation Hub, I used predictive models to evaluate the efficacy of two widely utilized MRC indices. Through these predictive analysis and other statistical comparisons, we explored the data to find the most effective metrics for predicting patient outcomes.

In this new project, I’ll show the power of bringing modeling techniques in healthcare analytics, for the application in MRC metrics. Although the sensitive nature of our data restricts me from sharing specifics or the precise analysis code, I will provide a thorough rundown of our methodological approach, the intriguing findings it yields, and the implications for future patient care.

Objective:

The objective of this study is to apply advanced statistical modeling techniques to assess and compare the predictive power of two commonly used Medication Regimen Complexity (MRC) indices for patient outcomes: MRCI & MRC-ICU.

Data:

This study recieved all proper ethical approval (see publication details), and used deidentified, retrospective data.

The retrospective cohort study at Roger William Medical Center, Providence, Rhode Island, included 317 adult patients admitted to the intensive care unit (ICU) between 1 February 2020 and 30 August 2020. It included detailed information on patient demographics, laboratory measurements, vitals, medications, and outcome including time on mechanical ventilation, length of stay in the ICU and mortality.

Data Processing:

MRCI and MRC-ICU were calculated according to the established criteria. We established cutoff values for both MRC scores based on their distribution within 24 hours of ICU admission. Since there are no standardized cutoff values specifically for critically ill patients, we selected the median values as our cutoff points. The “high” MRCI scoring cohort was defined as having scores greater than 63, while the “high” MRC-ICU cohort was defined as having scores greater than 6. We examined three clinical outcomes: mortality, length of stay (LOS), and the need for mechanical ventilation (MV) in the ICU. To assess LOS, we created a binary variable where LOS was labeled as 0 if it was less than 48 hours and 1 if it exceeded 48 hours. The need for MV was determined using a binary variable after 48 hours of ICU admission, with 0 indicating no mechanical ventilation and 1 indicating the use of mechanical ventilation. Hemodynamic instability was defined by the presence of hypotension (systolic blood pressure < 100 mmHg), mean arterial pressure below 65 mmHg, or abnormal heart rate (arrhythmia or heart rate below 60 bpm or above 100 bpm).

Descriptive statistics were employed to summarize the study population, presenting continuous variables as means and interquartile ranges (IQRs), and categorical variables as frequencies and proportions. Student’s t-test, chi-squared (χ²) test, or Fisher’s exact test were used to compare clinical characteristics between survivor and non-survivor cohorts, as well as low- and high-MRC-scoring groups. Physiological and clinical characteristics were examined among the survivor and non-survivor cohorts, and severity scores (SAPS II, APACHE II, and CCI) were incorporated

Analysis & Results:

To identify the predictors of clinical outcomes (mortality, length of stay [LOS], and need for mechanical ventilation [MV]), four multivariable logistic regression models were employed. These models included a combination of severity scores (APACHE II and SAPS II), Medication Regimen Complexity Index (MRCI), Medication Regimen Complexity in Intensive Care Unit (MRC-ICU), demographic variables, Charlson comorbidity index (CCI), and drug classes. Model I consisted of demographics, APACHE II, SAPS II, CCI, and 15 drug classes. Model II included demographics, MRCI at 24 hours and 48 hours, CCI, and drug classes. Model III incorporated demographics, MRC-ICU at 24 hours and 48 hours, CCI, and drug classes. Model IV encompassed all variables (refer to Table S3 for details). For the LOS models, MRCI and MRC-ICU values at 48 hours were excluded as the binary values were based on a 48-hour threshold after ICU admission. Significant predictors (p < 0.05) were selected using a stepwise forward selection method.

Feature selection was performed using an L1 penalization technique called LASSO, which minimizes the influence of multicollinearity. The demographic variables considered were age, sex, height, weight, body mass index (BMI), and race. Odds ratios (OR) were calculated for each outcome of interest. All analyses were conducted using R software, specifically Version 4.0.0 (R Project for Statistical Computing), and implemented packages such as glm, glmnet, and ggplot2.

The MRC scores, both MRCI (Medication Regimen Complexity Index) and MRC-ICU (Medication Regimen Complexity in Intensive Care Unit), showed significant associations with critical outcomes like mortality, length of ICU stay (LOS), and the need for mechanical ventilation (MV). This was similar to APACHE II and SAPS II scores, which are designed to predict mortality risk and the severity of disease.

To evaluate the prediction ability of MRC scores for mortality, LOS, and the need for MV, seven logistic classifier models were constructed without any variable selection. Correlation analysis was performed using the Pearson correlation coefficient, and the SAPS II severity score was chosen due to its high correlation with the APACHE II classification system (see Figure S1). The best-fit models were selected based on the best Akaike information criterion (AIC) measurement during cross-validation, employing an interactive process. All predictor variables were included in each prediction model setup to explicitly explore their individual roles. Model performance was assessed using the area under the receiver operating characteristic (ROC) curve (AUC), with an AUC of at least 0.7 considered acceptable. The models underwent a “leave-one-out” cross-validation method with 10,000 repetitions, and the AUC was selected as the overall performance measure. Sensitivity and specificity analyses were conducted for each of the three outcomes. Additionally, variable importance rankings were recorded for each clinical outcome in the prediction models.

The ROC analysis revealed that models incorporating Medication Regimen Complexity (MRC) scores alongside traditional severity scores like APACHE II and SAPS II demonstrated comparable or slightly superior predictive power, as evidenced by AUC values. These findings highlight the added value of MRC scores in enhancing model accuracy not only for mortality but also for predicting the length of ICU stay and the necessity for mechanical ventilation, suggesting that MRC scores capture additional patient risk factors not fully accounted for by physiological and clinical measures alone.

• Both Medication Regimen Complexity Index (MRCI) and Medication Regimen Complexity in Intensive Care Unit (MRC-ICU) scores were significantly associated with clinical outcomes, including mortality, length of stay (LOS), and the need for mechanical ventilation (MV).
• Higher MRC scores were linked to hemodynamic instability and higher severity scores, such as APACHE II and SAPS II.
• Survivors had significantly lower MRCI, MRC-ICU, APACHE II, and SAPS II scores compared to non-survivors.
• The addition of MRC-ICU and SAPS II scores improved the prediction accuracy of clinical outcomes.
• Hispanic ethnicity was identified as an important variable in predicting mortality, LOS, and the need for MV.
• The use of vasopressors, pulmonary agents, paralytic agents, and psychiatric medications significantly influenced clinical outcomes.
• The study findings suggest that MRC scores can be valuable in identifying high-risk patients and optimizing clinical management.
• Logistic regression models and logistic classifier models demonstrated the predictive capabilities of MRC scores for patient outcomes.
• The L1 penalization technique (LASSO) was used for variable selection, minimizing multicollinearity and improving prediction accuracy.
• The study highlights the importance of incorporating MRC scores into standardized severity index scoring tools to enhance the prediction of critical care outcomes.

Conclusions:

1. Medication Regimen Complexity (MRC) scores, including MRCI and MRC-ICU, are significantly associated with clinical outcomes, such as mortality, length of stay (LOS), and the need for mechanical ventilation (MV). These scores provide valuable insights into a patient’s health status and treatment course.

2. Higher MRC scores are linked to hemodynamic instability, higher severity scores, and poorer clinical outcomes. Monitoring and managing medication regimens based on MRC scores can help identify patients at higher risk and optimize their care.

3. Incorporating MRC scores, along with severity-of-illness scores like APACHE II and SAPS II, improves the accuracy of predicting clinical outcomes. This integration can enhance clinical decision-making and resource allocation in critical care settings.

4. The use of specific medications, such as vasopressors, pulmonary agents, paralytic agents, and psychiatric medications, significantly influences patient outcomes. Understanding the impact of these medications can guide medication selection and management strategies to improve patient outcomes.

5. The inclusion of MRC scores and medication-related factors in predictive models and statistical analysis provides valuable insights for clinicians and researchers. These models can assist in identifying high-risk patients, optimizing medication regimens, and improving patient-centered care.

6. The study emphasizes the need for standardized MRC scoring and the integration of MRC scores into clinical decision support tools. By incorporating MRC scores into electronic health records and clinical workflows, healthcare professionals can receive alerts and recommendations for medication review and safer patient care.

7. Future research should focus on validating the findings using larger patient cohorts and diverse populations. Additionally, exploring the role of MRC scores in specific high-acuity diseases and evaluating the impact of interventions based on MRC assessments would further enhance our understanding of medication regimen complexity and patient outcomes in critical care settings.

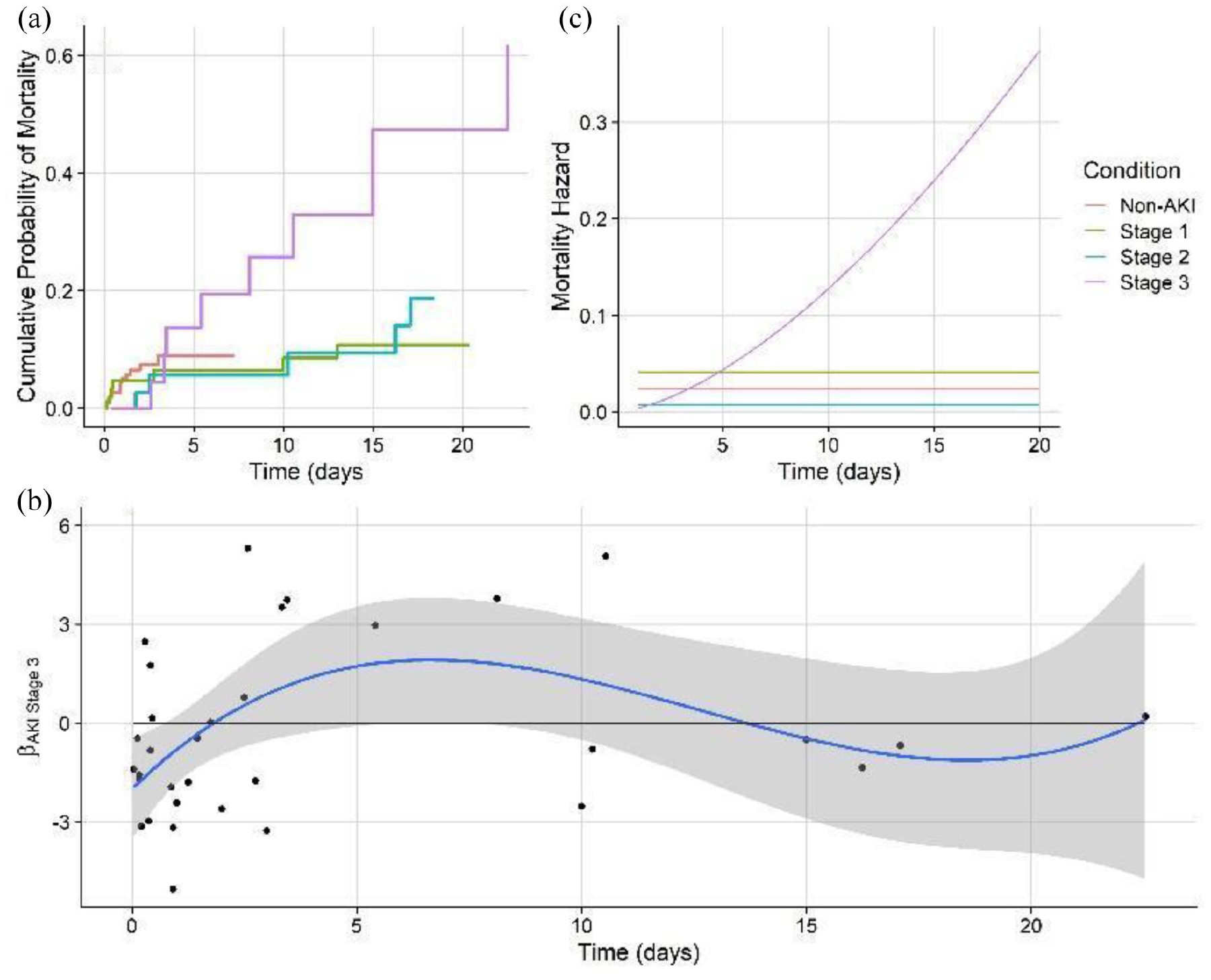
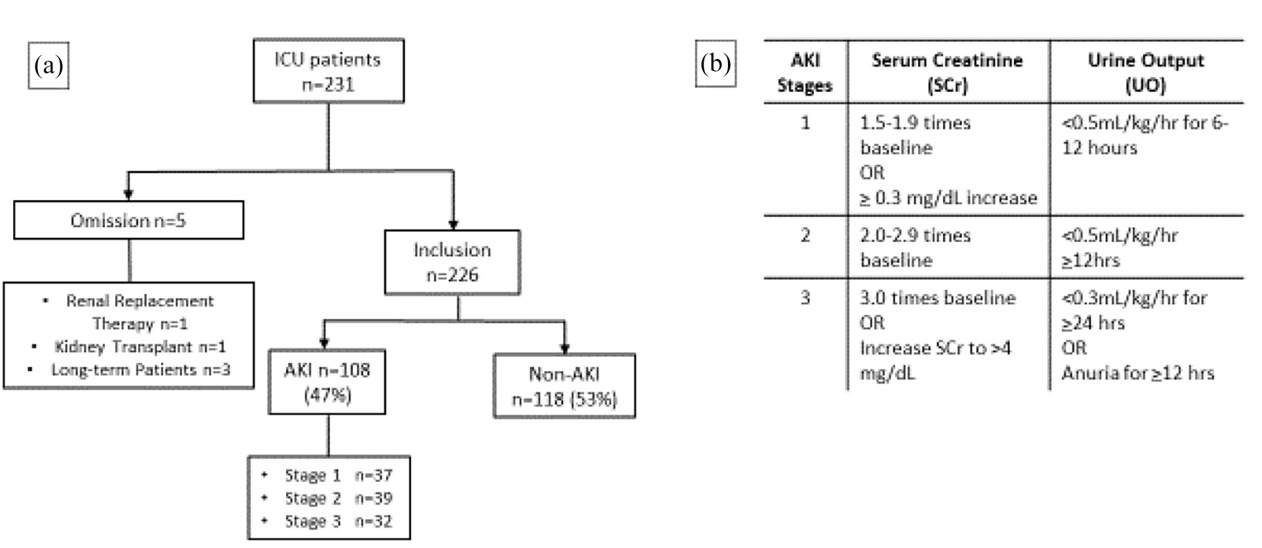
There are two data attributes which are nearly ubiquitous but often under-appreciated and misunderstood. The first is time: a dimensions which is physically unavoidable, but often ignored to the detriment of predictive power and insight. The second is missing data: a true nuisance for analysis which can also easily become a major pitfall. This is especialy true if, as is often done, overly simplistic methods are relied on and thus major statistical bias introduced.

These ubiquitous and misunderstood attributes have fascinated me on countless projects, but stand forefront on analysis I developed working to unravel climate signals in a multi-decadal environmental series of environmental data. In this project, I looked to analyze how nutrient pollution had changed over decades in Narragansett Bay, across policy changes, and how this had affected the algae (aka phytoplankon) that make the base of the food-web, are responsible for eutrophication, and toxic bloom events.

Though the series is unprecidented in length (>60 years to date), the data has major challenges that require careful design. Missing data is present throughout the series in some cases with durations > 1 year, posing a challenge for unbiased inference. Further the changes to the underlying system, mean we expect the dependence structure evolves through time. Plainly, by this I mean coefficients, covariance, variance, etc. are unlikely to be static along the time dimension, and need to be able to change to describe changing relationships and structure.

Though, I will briefly summarize my work here, you can read my 133 page thesis about it (embedded below)… or read my publication in Statistics and Its Interface, both of which will cover both greater breadth and depth.

Objective:

1. Identify the long-term patterns in key environmental traits & identify the impact of policy change
2. Characterize the seasonal and long-term dependence of algal growth on nutrients
3. Develop a specialized architecture for inference with Bayesian dynamic linear models where missing data imputation is necessary and multiple modeling goals may be required

Data:

The data for this study come from the University of Rhode Island, Long-term Narragansett Bay Monitoring Series (2003-2020). Within this period, from 2005-2012, Rhode Island law mandated a 50% reduction in nutrient pollution from coastal wastewater treatement centers, and a major question as to the efficacy of this action.

Temperature, NH₄ (ammonium), NO₃ + NO₂ (nitrate + nitrite), chlorophyl (chl) <20 μm, chl > 20 μm were the measured features of the series. The chemical variants of nitrogen are known pollutant types to affect algal growth, and the algae itself is measured via it’s dominant pigment (chlorophyl a). The algal measurements are divided on size because of the major effect of size on ecosystem function in everything from food-web interactions to carbon sequestration. Thus, through these measures we hope to see how relevant nutrient polution has changed, and the effect on algae.

Data Processing:

The only processing taken before model development and fit is to perform a natural log transformation on nutrient and chlorophyll levels, simply to reduce skew in the data and meet Gaussian distribution assumptions for model errors. All other attributes with the data (e.g., missingingess, heteroskedasticity in time) I handled with the model architecture.

Analysis and Results

As described above, there are several key applied goals for the environmental series which are made difficult in particular by missing data. Ultimately, the technique I develop is with a multistage model where the first stage serves to analyze univariate time-series traits, and impute missing data with uncertainty, and a second stage is developed to target questions which are multivariate in nature (i.e., how algal biomass is affected seasonally and in the longterm by nutrient pollution).

The General DLM Structure

The core of the modeling approach is the Bayesian dynamic linear model (or DLM), a popular time-series tools which model our data as observations of a latent state evolving through time according to an observation and state equation (eqns. 1, 2). These models have an inherent ability to imput missing data through forward filtering with the Kalman filter followed by backward sampling (Kalman 1960).

Equation 1. Observation equation:

Equation 2. State equation:

Kalman Filtering and Smoothing:

1. One-step-ahead predictive distribution of the latent state, \(f(\Theta_t \vert y_{1:t-1}) = N(a_t, R_t)\) where:

   \[a_t = E(\Theta_t|y_{1:t-1}) = G_t m_{t-1}\] \[R_t = Var((\Theta_t|y_{1:t-1})) = G_t m_{t-1} G'_t + W_t\]

2. One-step-ahead predictive distribution of the observation, \(f(Y_t \vert y_{1:t-1}) = N(f_t, Q_t)\), where:

   \[f_t = E(Y_t \vert y_{t-1}) = F_t a_t\] \[Q_t = Var(Y_t \vert y_{t-1}) = F_t R_t F'_t + V_t\]

3. The filtered distribution of the latent state, \(f(\Theta_t \vert y_{1:t}) = N(m_t, C_t)\), where:

   \[m_t = E(\Theta_t \vert y_{1:t}) = a_t + R_t F'_t Q^{-1}_t e_t\] \[C_t = Var(\Theta_t \vert y_{1:t}) = R_t - R_t F'_t Q'_t F_t R_t\] \[e_t = Y_t - f_t\]

4. The smoothed distribution of the latent state, \(f(\Theta_t \vert y_{1:T})=N(s_t, S_t)\), where:

   \[s_t = E(\Theta_t \vert y_{1:T}) = m_t + C_t G'_{t+1} R'_{t+1}(s_{t+1} - a_{t+1})\] \[S_t = C_t - C_t G'_{t+1}R^{-1}_{t+1}(R_{t+1})R^{-1}_{t+1}G_{t+1}C_t\]

These models also allow any parameter of our model to time vary, allowing us to study temporally changing relationships. This includes covariance matrices through a method called discount factoring. This method works extremely well for dynamic covariance when data are mostly complete. The method, outlined in West and Harrison 1997, mathematically suggest that the covariance matrix \(W_t\) for the latent state specification of the model, should decay from one time step to the next.

The DLM itself, like a NN or regression is just a general framework to which we can adapt to very specific architecture. Through the general system of equations shown above, very detailed solutions are possible, for example, ARIMAX or dynamic regression are popular architectures. In our case, we build architectures specifically to answer our questions in each of the stages.

Stage 1 Architecture

In stage 1, we setout to answer questions about long-term patterns such as seasonality, and the long-term trend. Thus we can build a structure which specifically includes these components. In the parameterization outlined below, each time-series is modeled with a dynamic intercept (long-term trend, \(\mu\)), and Fourier form seasonal components from a period of 1 year to 23 weeks to capture complex seasonal patterns.

Stage 2 Architecture

In the second stage, the goals is to determine the dependence structure between nutrients and algal biomass. Rather than try to model the series entirely with trend and seasonal components, we try to quantify the impact of an exogenous predictor. The second stage model also includes a dynamic intercept, a annual cycle with a period of 1 year, and a dynamic regression component on nitrogen sources. In this way, the model tells us how nitrogen predicts the anomaly from bulk seasonal and long-term patterns which are affected by a plethora of other traits.

Model Fit

The model was fit with Markov-chain monte-carlo to solve for the posterior distribution of each parameter. It’s worth noting that the method of dividing the modeling into two stages allowed the MCMC inference to be carried out independently for each stage. This separation meant that the posteriors from stage 1 could be sampled in stage 2, and the inference on missing data did not need to be repeated in the regression analysis. This added efficiency to the model fitting process.

Results

The study presents a two-stage Dynamic Linear Model (DLM) as a versatile tool for handling noisy, incomplete, and non-monotonic time-series data in long-term environmental monitoring. In this work:

• I successfully applied a new multistage DLM architecture to assess the relationship between phytoplankton populations and dissolved inorganic nitrogen (DIN) levels in the Narragansett Bay.
• The first stage of the model allows characterization of seasonal and long-term change in the data and supports inference into periods of missing data. The completed data series helps in further exploratory analysis.

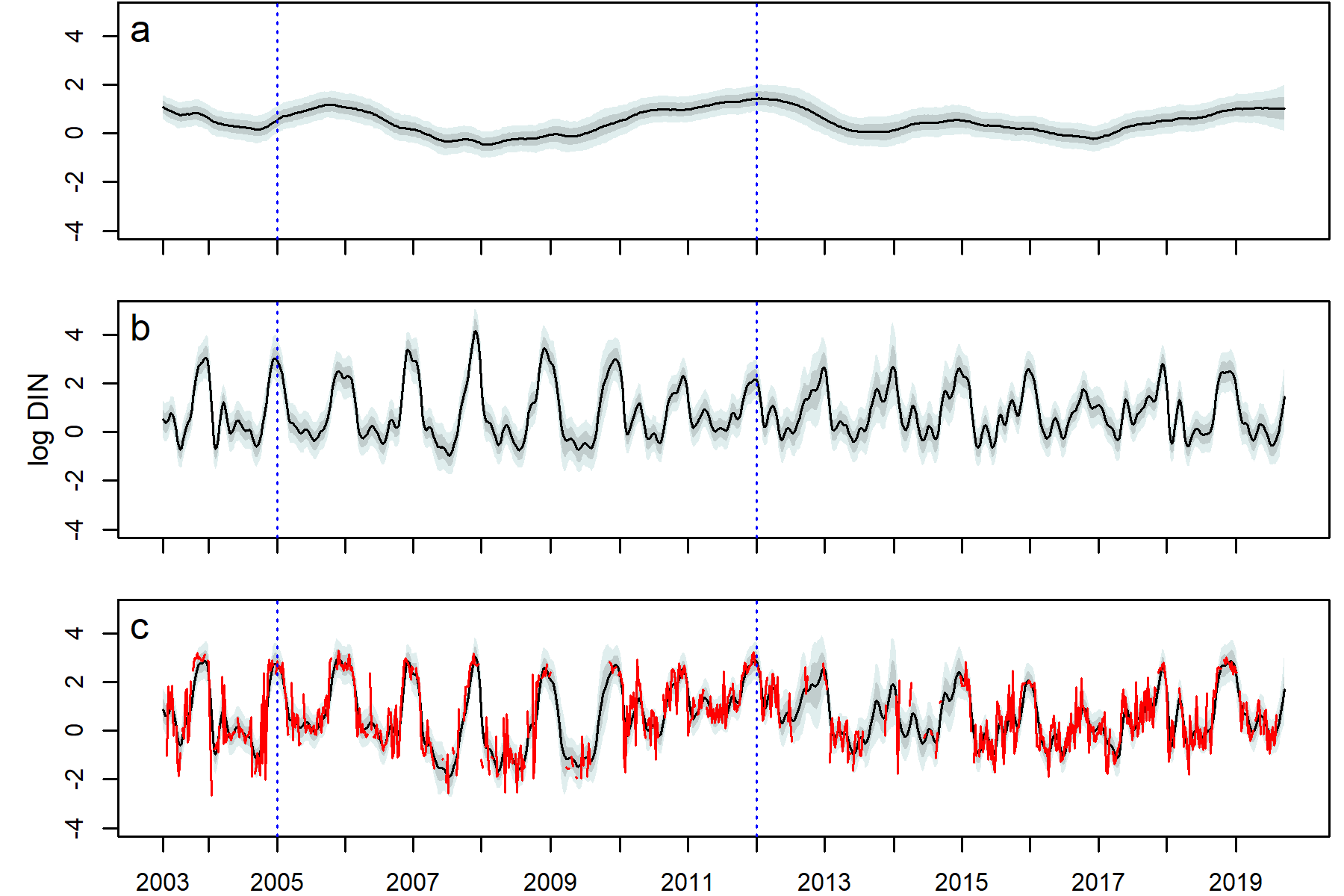
Decomposition of the DIN series DLM (2003–2019), fit with the stage 1 model structure. a. the dynamic intercept, b. the seasonal trend, c. the posterior predicted mean with the true data (red). The median (black), 80% (dark grey shading), and 95% (light grey shading) pointwise credible intervals are shown. Blue dotted lines denote the beginning and end years of policy mandated nutrient remediation.

• The second stage of the model focuses on dynamic regression, working with the latent levels of the predictors, which are devoid of observational uncertainty. This stage examines the dependencies between the studied variables.

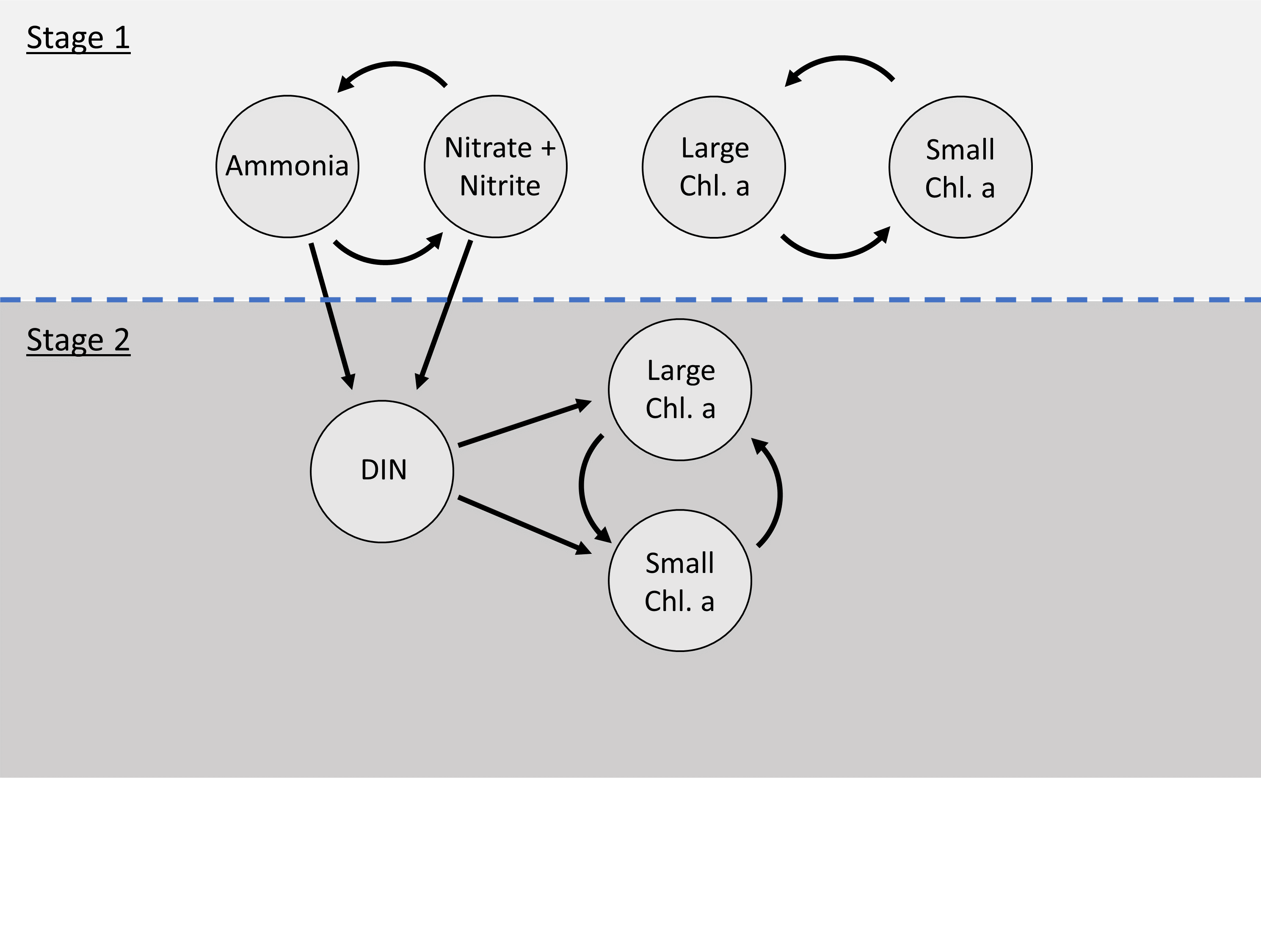
Dependence structure between components of the stage 1 and stage 2 model for the Narragansett Bay ecological model. A bivariate model was run for small and large chl. a as well as nitrate + nitrite to describe long-term patterns among all series. Examination of prewhitened cross-correlations between the imputed series after stage 1 led to the use of DIN as a predictor in stage 2 to explore the influence of nitrogen on size structure of phytoplankton. Stage 2 used latent levels of ammonia and nitrate + nitrite.

• Practical discount methods were found critical for the evolution covariance matrix, preventing over-parameterization and mixing issues in the Markov Chain Monte Carlo (MCMC) algorithm, which is used for estimation and inference in the DLM.

• The multistage DLM allows for the MCMC inference to be carried out independently for each stage, improving computational efficiency by not repeating the inference on missing data in the regression analysis.

• Ultimately, this model answered the key question on how algae blooms were effected by the policy changes. Results suggest that smaller phytoplankton (<20 μm) are relatively unaffected by changes in DIN levels, while larger phytoplankton (>20 μm) show a negative relationship with DIN. This relationship varies seasonally, with the strongest associations occurring in the winter.

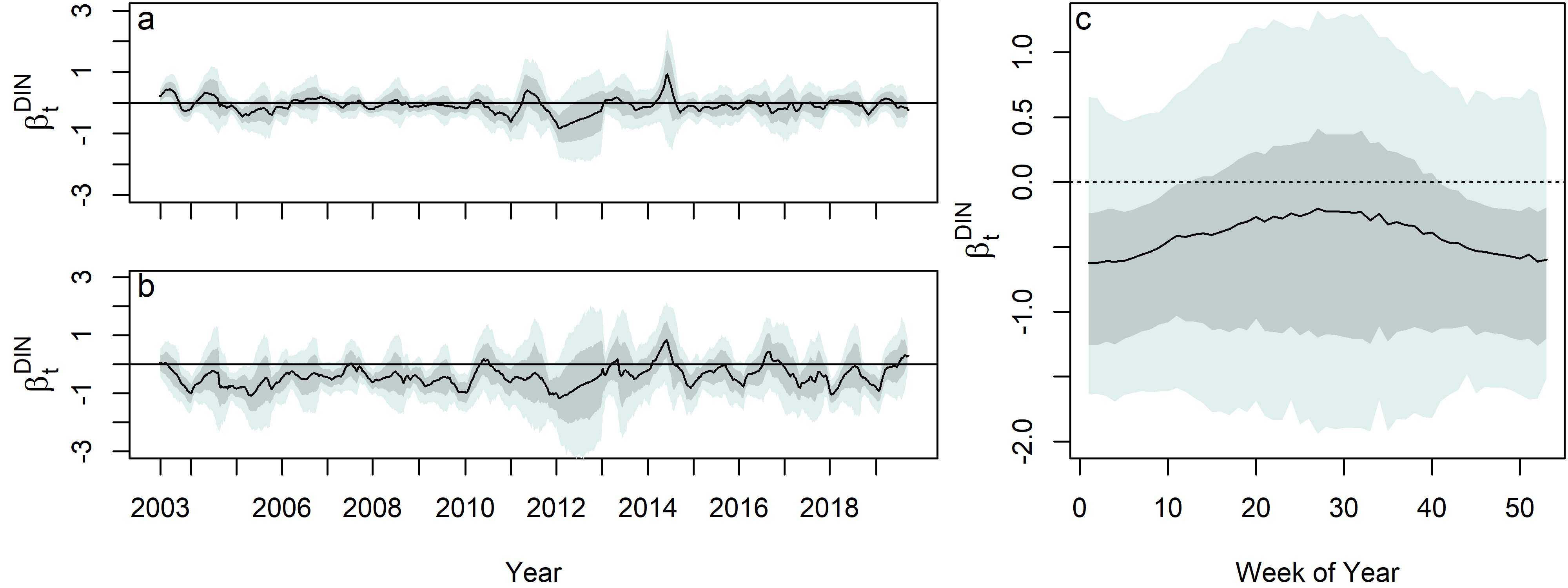
The dynamic regression coefficient, $\beta^{DIN}_t$ , for both the a. Small chl. a series b. Large chl. a series. c. Posterior distribution of the dynamic regression coefficient, $\beta^{DIN}_t$ , on DIN for the large chl. a, plotted by week on the x–axis, and by year as denoted by color shading. The median (black), 80% (dark grey shading), and 95% (light grey shading) are shown.

• The multistage DLM can accommodate data with significant missing points, disparate data streams, and multiple modeling goals.

• The multi-stage state-space model architecture shows value for environmental monitoring and similar long-term analyses.

Conclusions:

• Policy changes did not have a statistically distinguishable effect on Nitrogen levels at the study site (though other research has found localized effects closer to the sources).

• The size of algal organisms shifted from being dominated by large to being dominated by small organisms, which could potentially impact everything from food-web structures to carbon sequestration.

• The dependence on nitrogen has not significantly changed, and is highly seasonal, meaning seasonally targeted efforts, especially in the winter could have the greatest effect on algal growth.

• Practical discounting methods, though previously untested, show superior accuracy for imputation in cases of non-static covariance.

• The multi-stage architecture is particularly advantageous for modeling efforts with multiple goals and extensive missing data. With this architecture, the first stage can server to both characterize the time-series and provide advanced multiple imputation, leaving the flexibility to experiment in the second stage with a more parsimonious model.

Time series analysis and time series of data are powerful for building our understand on a topic, but there is almost invariably a big challenge: missing data. Measuring devices brake, data collection is interupted, and periodically the funding may dry up. The way that we handle this missing data can have large effects and potential biases for our inference.

Bayesian state-space models and the particular case of the dynamic linear model are popular time-series tools which model our data as observations of a latent state evolving through time according to an observation and state equation (eqns. 1, 2). These models have an inherent ability to imput missing data through forward filtering with the Kalman filter followed by backward sampling (Kalman 1960).

Equation 1. Observation equation:

Equation 2. State equation:

Kalman Filtering and Smoothing:

1. One-step-ahead predictive distribution of the latent state, \(f(\Theta_t \vert y_{1:t-1}) = N(a_t, R_t)\) where:

   \[a_t = E(\Theta_t|y_{1:t-1}) = G_t m_{t-1}\] \[R_t = Var((\Theta_t|y_{1:t-1})) = G_t m_{t-1} G'_t + W_t\]

2. One-step-ahead predictive distribution of the observation, \(f(Y_t \vert y_{1:t-1}) = N(f_t, Q_t)\), where:

   \[f_t = E(Y_t \vert y_{t-1}) = F_t a_t\] \[Q_t = Var(Y_t \vert y_{t-1}) = F_t R_t F'_t + V_t\]

3. The filtered distribution of the latent state, \(f(\Theta_t \vert y_{1:t}) = N(m_t, C_t)\), where:

   \[m_t = E(\Theta_t \vert y_{1:t}) = a_t + R_t F'_t Q^{-1}_t e_t\] \[C_t = Var(\Theta_t \vert y_{1:t}) = R_t - R_t F'_t Q'_t F_t R_t\] \[e_t = Y_t - f_t\]

4. The smoothed distribution of the latent state, \(f(\Theta_t \vert y_{1:T})=N(s_t, S_t)\), where:

   \[s_t = E(\Theta_t \vert y_{1:T}) = m_t + C_t G'_{t+1} R'_{t+1}(s_{t+1} - a_{t+1})\] \[S_t = C_t - C_t G'_{t+1}R^{-1}_{t+1}(R_{t+1})R^{-1}_{t+1}G_{t+1}C_t\]

These models also allow any parameter of our model to time vary, allow us to study temporally changing relationships. This includes covariance matrices through a method called discount factoring. This method works extremely well for dynamic covariance when data are mostly complete. The method, outlined in West and Harrison 1997, mathematically suggest that the covariance matrix \(W_t\) for the latent state specification of the model, should decay from one time step to the next.

Discounting Covariance:

Practically, this equation represents how the information is lost from one time step to the next.

The issue is that for data with extended periods of missingness, standard discounting methods would have the loss of information grow at an exponential rate in the forward filter. If we are predicting \(k\) steps ahead with data, then the covariance at step \(k\) ahead becomes:

This is as opposed to a linear rate in a static covariance specification that comes with the Kalman filter above:

Inutition suggests that an exponential loss of information in missing data may be overly conservative, but what covariance specification gives us the most accurate results for periods of extensive missing data?

Further, what is the optimal selection criteria for selecting a discount factor?

Objectives:

1. Identify the optimal discounting strategy for prolonged periods of missingness

2. Identify the criteria with the strongest statistical power to compare models with different configurations such as fixed discount factors.

Data :

This theoretical investigation was spurred by real time series data from the Narragansett Bay Long-term Time Series. I will use the log transformed Chlorophyll (algal pigment data), because it is the subject of another time series analysis I have been working on. The data is from 2003 to 2020, collected at weekly resolution. While the use of a multivariate analysis would be optimal for imputation, I use a univariate series to focus on the question of covariance specification.

Raw data can be found here.

Data Processing:

While it might seem counter-intuitive, I am using the real data from the time-series to parameterize known data generation models. I choose to do this over completely random data generation models becuase this theoretical investigation is directly tied to the applied problem of analyzing the real data with heteroskedastic behavior and prolonged missingness.

The data were first logged transformed due to their highly positively skewed nature. Second, a dynamic linear model was fit to the data. To capture long-term trend and seasonal behavior, the latent state contained a dynamic intercept and fourier form seasonal components. The models were fit with different levels of fixed discount factors. The posteior mean of \(V\) and \(W_t\) was calculated. New data series were generated from each model fit, with known parameterization. In each copy of the simulated series, missingness was randomly introduced with a frequency distribution matching the original data.

Analysis & Results:

With the simulated data, DLMs were fit with different discount factor levels. The idea is to see if we can recover the discount factors of the data generation model, and which performance criteria helps us make this recovery with the highest accuracy and statistical power. Six performance metrics were calculated and compared to identify which most strongly identified the correct data generation structure.

Performance metrics were compared between fits with practical and standard discounting.

For the data generation model of high discount factors our performance metrics are the following for each model fit, where the x-axis is a set of discount factors used in a model fit:

For the data generation model of low discount factors our performance metrics are the following for each model fit, where the x-axis is a set of discount factors used in a model fit:

Comparing the standard and practical discounting methods we find the following for each data generation model:

Conclusions:

• Under data simulated with a pair of high discount factors (0.999, 0.99), all metrics selected within 0.009 of the parameters for data generation
• Consistently, $RMSFE_1$ had the most statistical power to recover the parameterization of the data generation model.
• $RMSE$ suggests practical discounting will optimize performance in long-periods of missingness
• DIC support practical discounting imporves the model fit within sample
• Although $RMSE$ was a biased metric for model selection, particularly during prolonged periods of missingness, it still had utility in evaluating the performance of practical discounting in data with long period missingness.
• While $RMSFE$ may be the optimal method for discount factor selection, it does not account for performance during longperiod missingness as our metric of RMSE does. Therefore, results of RMSE in comparable models with practical and standard discounting provide an evaluation for this imputation method.

Literature Cited:

Kalman, R. E. 1960. “A New Approach to Linear Filtering and Prediction Problems.” Journal of Fluids Engineering, Transactions of the ASME 82 (1): 35 45. https://doi.org/10.1115/1.3662552.

West, Mike, and Jeff Harrison. 1997. Bayesian Forecasting and Dynamic Models . 2nd ed. Verlag New York: Springer. https://doi.org/10.1007/b98971.

Marine microbes are some of the most numerous organisms in the world. Although you may have never seen or though about them, they make our planet survivable in many ways (not the least of which is producing 50% of the atmospheric oxygen we breathe and forming the base of the food we in all the world’s oceans). Despite being so numerous and critical to life on our planet, there are major gaps in our understanding of how these tiny organisms are shaped by their environment.

Under a fellowship with NASA Space Grant, I studied how temperature impacts these critical organisms. In this project, by creating mathematical models of microbial growth and size as a function of temperatures, I provided a small piece of NASA’s large numerical models that work to model and predict our own planetary function.

If you would like the full details of the published study, you can read it here:

Objective:

Measure the growth and cellular size traits of a globally relevant marine algae.

Mathematically model how the cellular traits are impacted by temperature. Use interpretable statistical models that can be used for prediction and ecological interpretation. From the start, we had several targeted questions:

1. How do populations of microbes grow across a wide range in temperatures?
2. How are the sizes of the microbial cells impacted across a wide range in temperature?
3. How much do changes in temperature (thermal perturbations) impact population growth?
   • Does the impact from change itself impact our ability to estimate temperature effects?

Use ocean thermal data and mathematical models of thermal responses to estimate the magnitude of thermal effects on microbial function.

Data:

Cells and Culture Growth

As a study case for the biological response of algae to temperature and temperature change, I chose an algae which is both common and toxic, Heterosigma akashiwo. The cells were kept healthy, in exponential growth. To avoid convolution of the thermal response with the response to new media, cultures were only transferred to new media more than 1 d prior to and 1 d post to a change in temperature.

Temperature treatments

With little prior information as to which features of changing temperature might influence growth, two major traits were examined in the experimental design: (1) the direction of temperature change (increasing or decreasing) and (2) the magnitude of temperature change (small shifts vs. larger cumulative changes). To address these features, and represent realistic rates of change, cultures were shifted sequentially to new growth temperatures outward from 15\(^{\circ}\)C (Fig. 1). Including the control culture, growth rate, and acclimation was measured at 10 temperatures: 6\(^{\circ}\)C, 8\(^{\circ}\)C, 10\(^{\circ}\)C, 12\(^{\circ}\)C, 15\(^{\circ}\)C, 18\(^{\circ}\)C, 22\(^{\circ}\)C, 25\(^{\circ}\)C, 28\(^{\circ}\)C, and 31\(^{\circ}\)C. As each incubator had a static temperature, we used small discrete shifts in temperature over time. Beginning with the culture that was acclimated to 15\(^{\circ}\)C, every 4 d a triplicate set of the cultures growing at the highest and lowest current temperatures were split, with one fraction retained at its current temperature and the other fraction shifted one temperature step outward (i.e., further toward the temperature extremes of 6\(^{\circ}\)C and 31\(^{\circ}\)C.

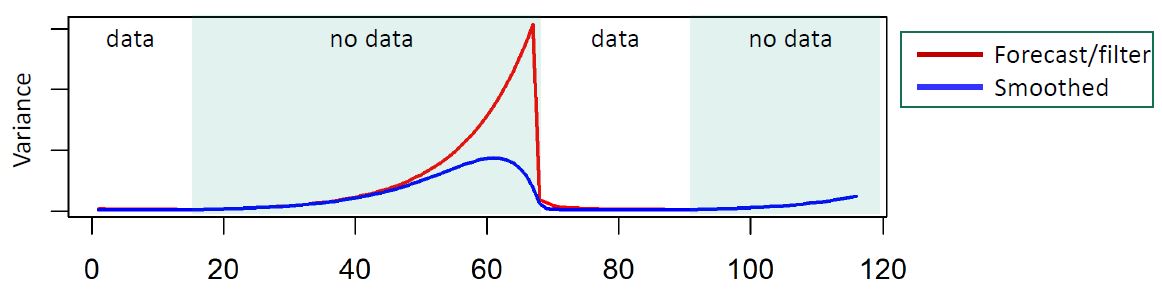
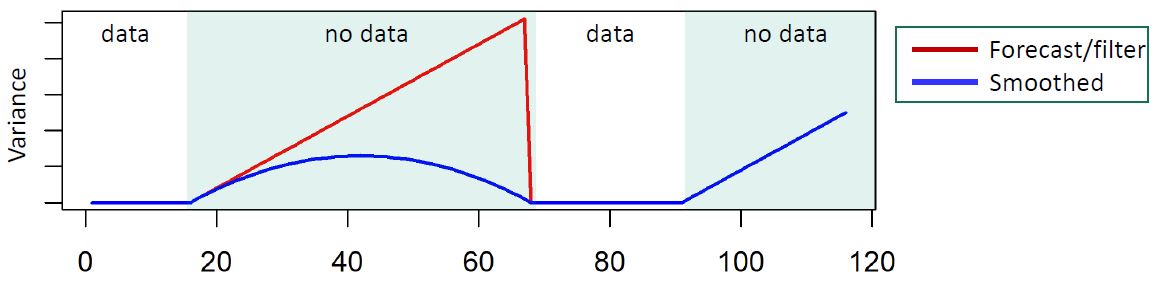
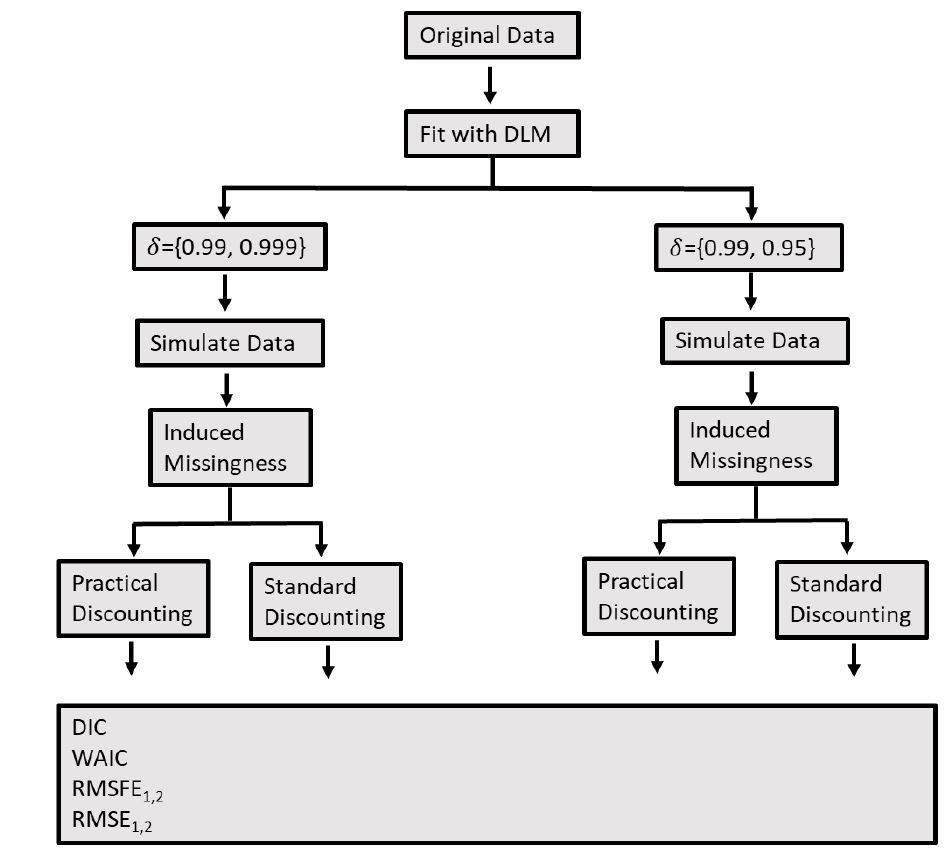
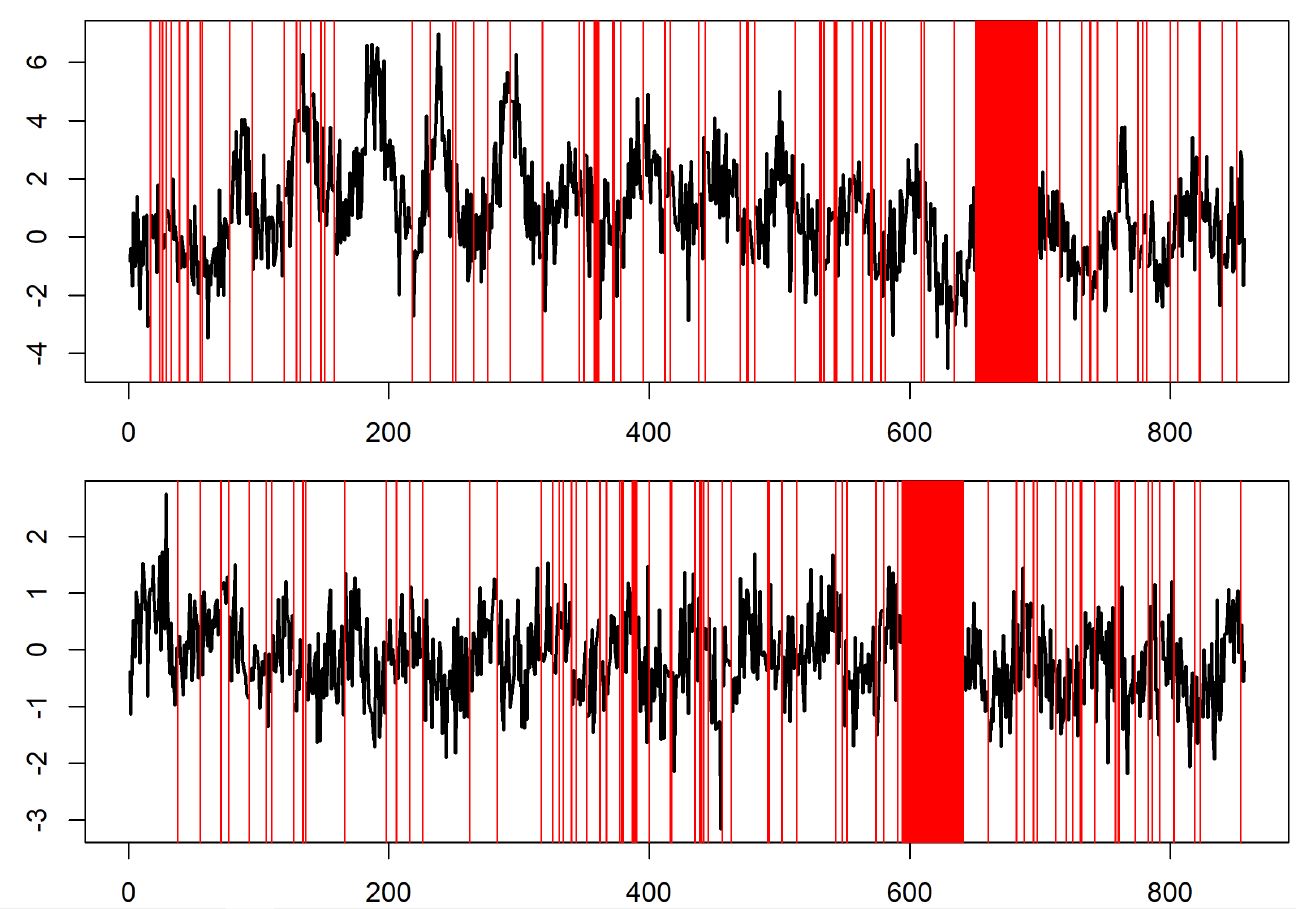
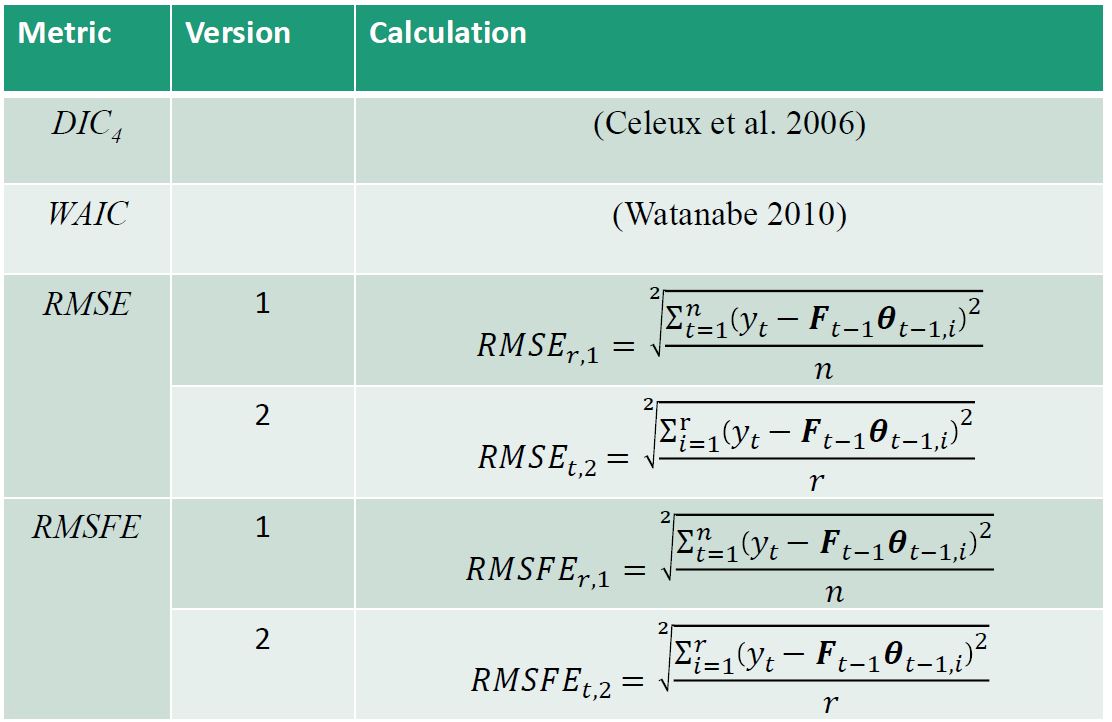
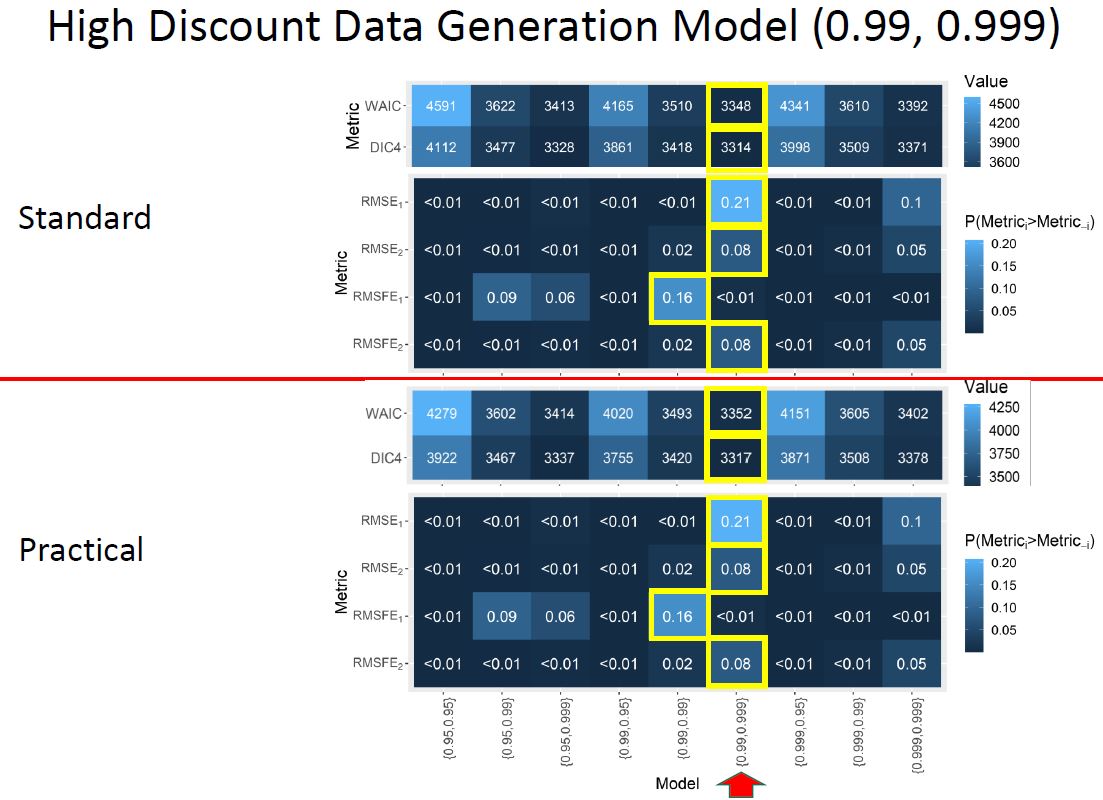
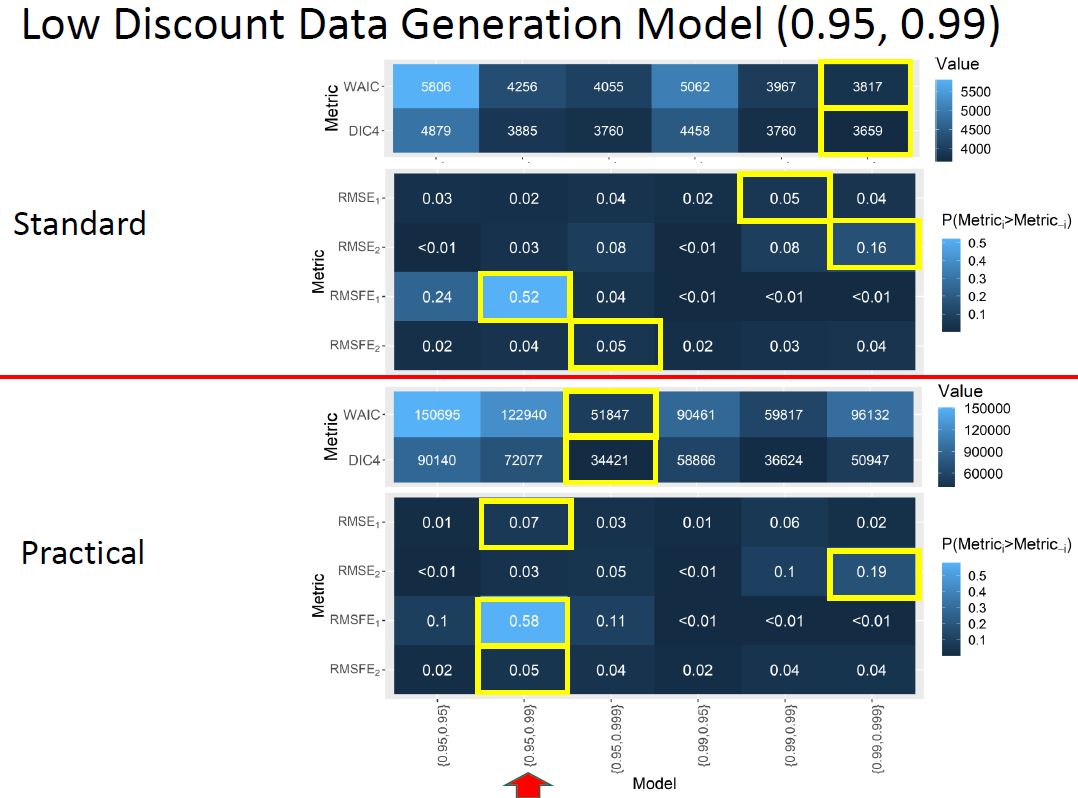
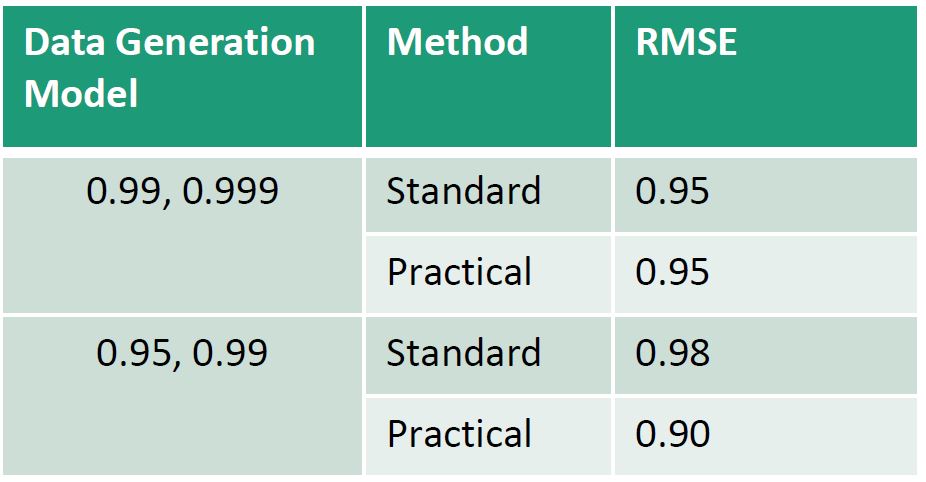
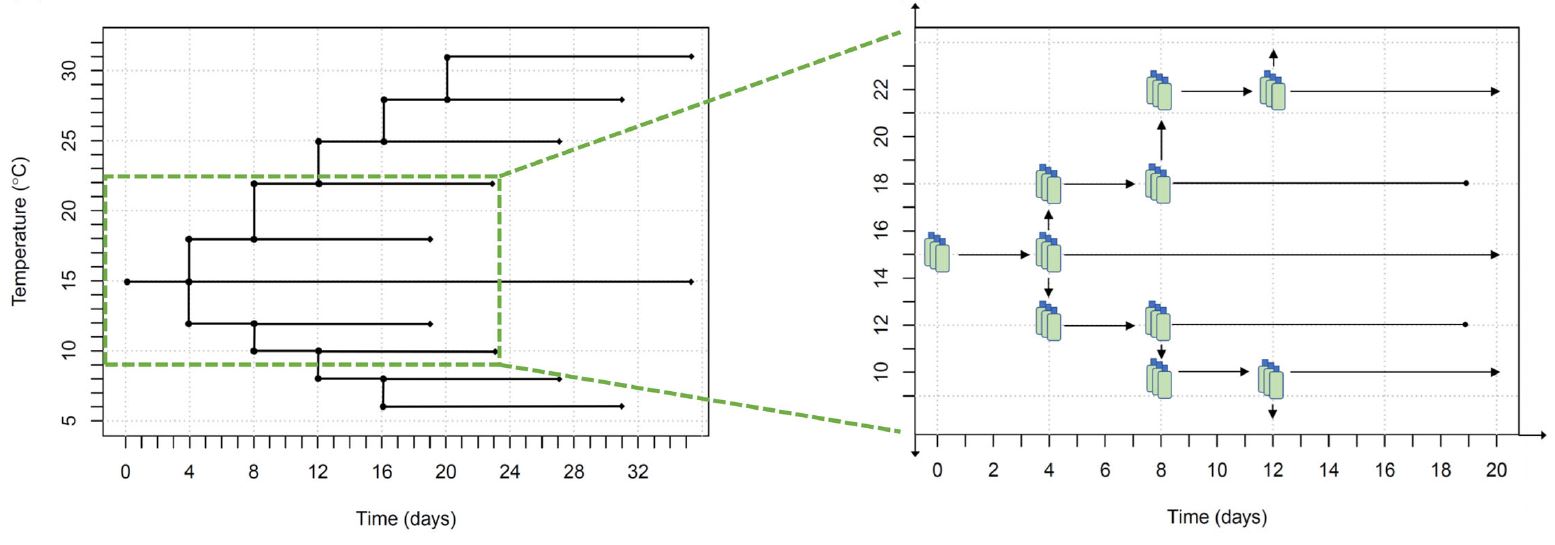Figure 1: Experimental temperature treatement design and temporal component to data collection.

Data Collection

To quantify changes in cell size, population growth rate (cell numbers), and volumetric growth rate, the abundance and cell size distribution were measured with a Beckman Coulter Multisizer 3 for 15 d following the initial transfer to the target temperature.

Data Processing:

The measurement taken in this study, for which, all statistics are derived are cell size distributions. The Coulter counter is a machine which counts the number of particles in size bins from ~1 to 100 \(\mu\)m. Measuring the number of cells in culture with automated instruments, can be produce suprisingly noisy data that need to be cleaned. Particularly, decaying material and undesireable cell populations in the culture may show signals in the data.

While normally the data are processed by hand, I automated the processing of thousands of cell distributions by fitting a mixture of a Gaussian and exponential mixuture model to the cell size distribution data, I quantified the mean and variance of the size distribution and number of cells in the target population. The traits of these population measures served as the key independent varaibles in the desired mathematical models of growth. Below you can see an example of a cell size distribution with overlaid Gaussian density curves:

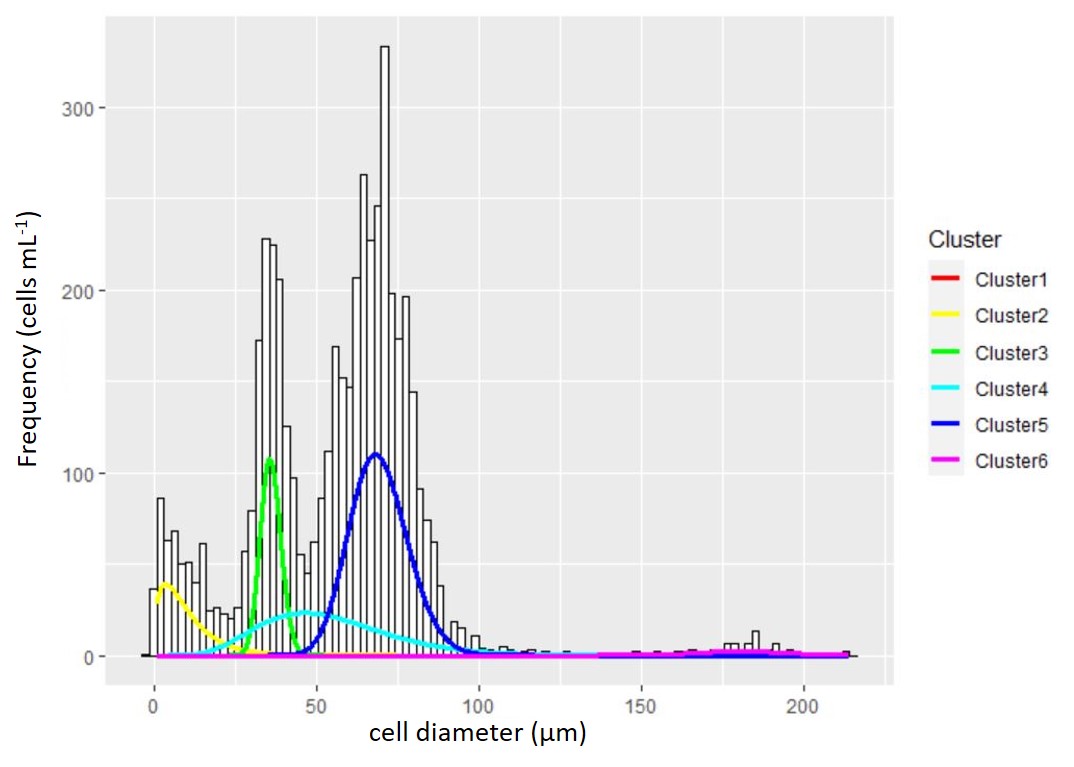Figure 2 : A particle and cell size distribution is fit with a mixture of distributions to identify the true cell count and population characteristics. The raw data collected from the Coulter counter is the underlying histogram of cell size with frequency on the y-axis and cell size on the x-axis. To fit the mixture distribution, the frequency data is first converted to raw measurements of individual cells. The density distributions from the mixture model are overlaid for graphical reference to the model fit. Unlike most clustering cases where the true number of clusters cannot be known, microscopy was used to verify the number of true cell populations and possibly multiple cell size groups of the same population.

Population growth rates were calculated by fitting an exponential growth curve to the population data:

where:

• \(P_t\) is the population at time \(t\)
• \(P_0\) is the original population
• \(r\) is the growth rate
• \(t\) is the elapsed time

Analysis & Results:

1.) How does temperature affect growth rate?

With maximum likelihood estimation, I used the calculated specific growth rates were to fit a standard thermal reaction curve used in biology:

where :

• a, b, and z are shape parameters
• w is the thermal niche width
• T is a given temperature
• k(T) is the specific growth rate at that temperature

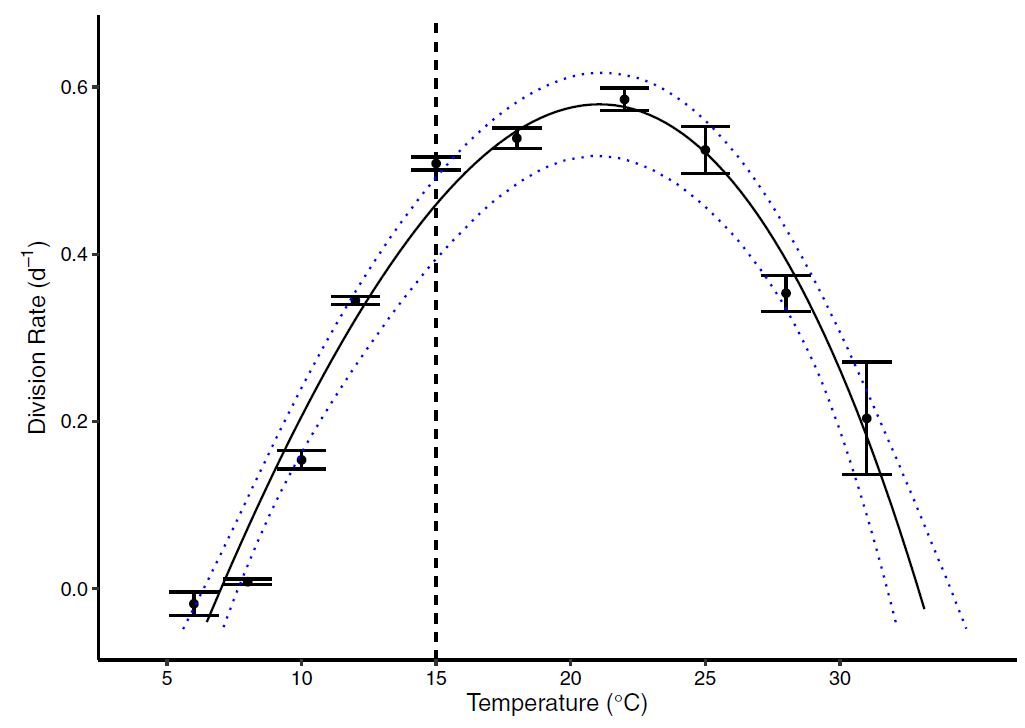Figure 3 : The thermal reaction norm showed a clear thermal dependence with a tolerable range (\(w = 25.9^{\circ}\)) spanning from \(7^{\circ}C\) to \(33^{\circ}\). This upper temperature range suggests that the marine algae can survive to some of the hottest temperatures seen in the ocean, and are likely to tolerate further warming with continued positive growth rates. However, warming beyond the optima (\(z=20^{\circ}C\)) will result in thermal stress.

2.) How are the sizes of cells impacted by temperature?

And analysis of cell size showed that both the devision rate and cell size were closely tied to temperature:

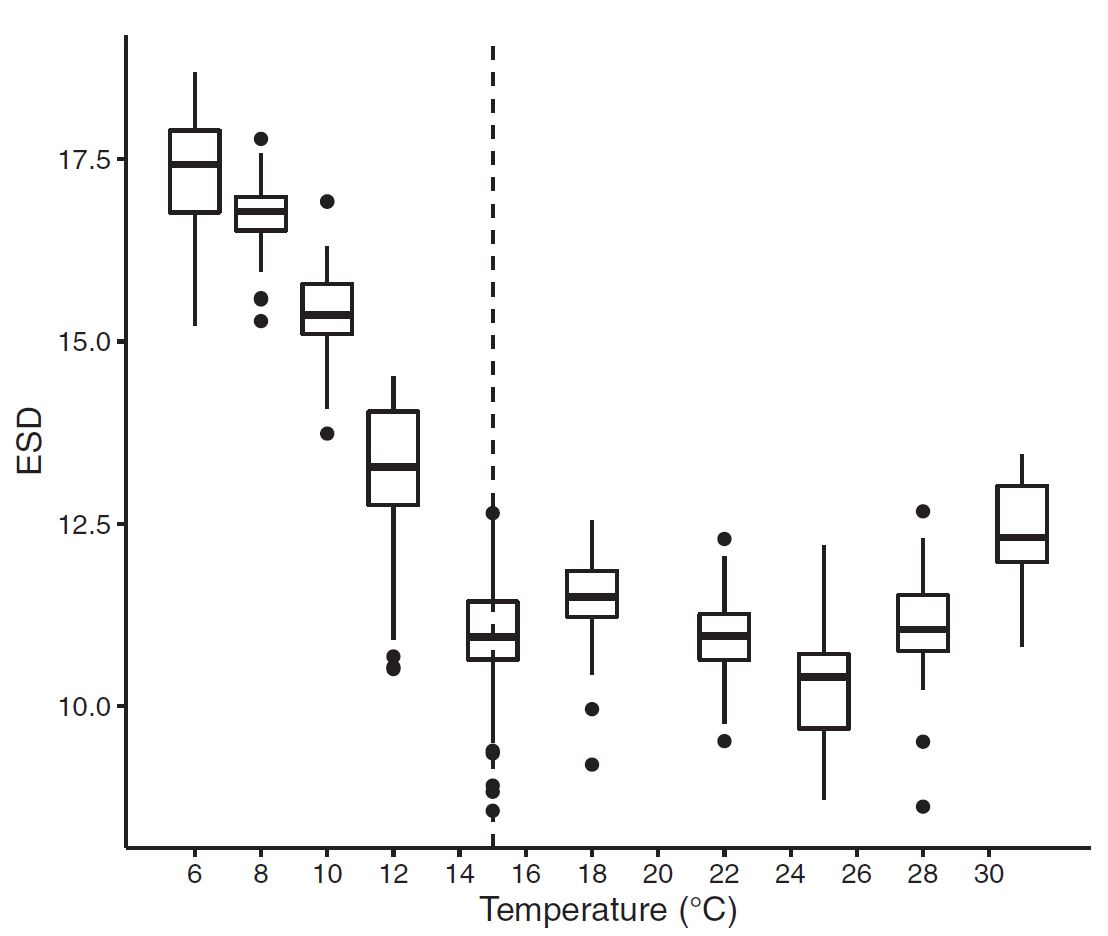Figure 4: ESD (Cell diameter) measurements across temperature. Results show a clear relationship with generally decreasing cell size as temperature increases.

While the relationship between cell size and temperature is strong, nuance here is important. From the graphical outputs, I had noted, the cell size relationships and aberations from linearity seemed to match an inverse of the temperature growth curve. After noting some-nonlinearity in the relationship, and conducting other exploratory comparisons, I tested whether there was another explainatory reason for cell size changes.

After comparing multiple models (AIC) with a type II regression, I showed that cell size was best explained by cell division rates. This is important to our understanding because the evidence suggests that it’s not temperature directly, and potentially any influences on division rates will affect cell size.

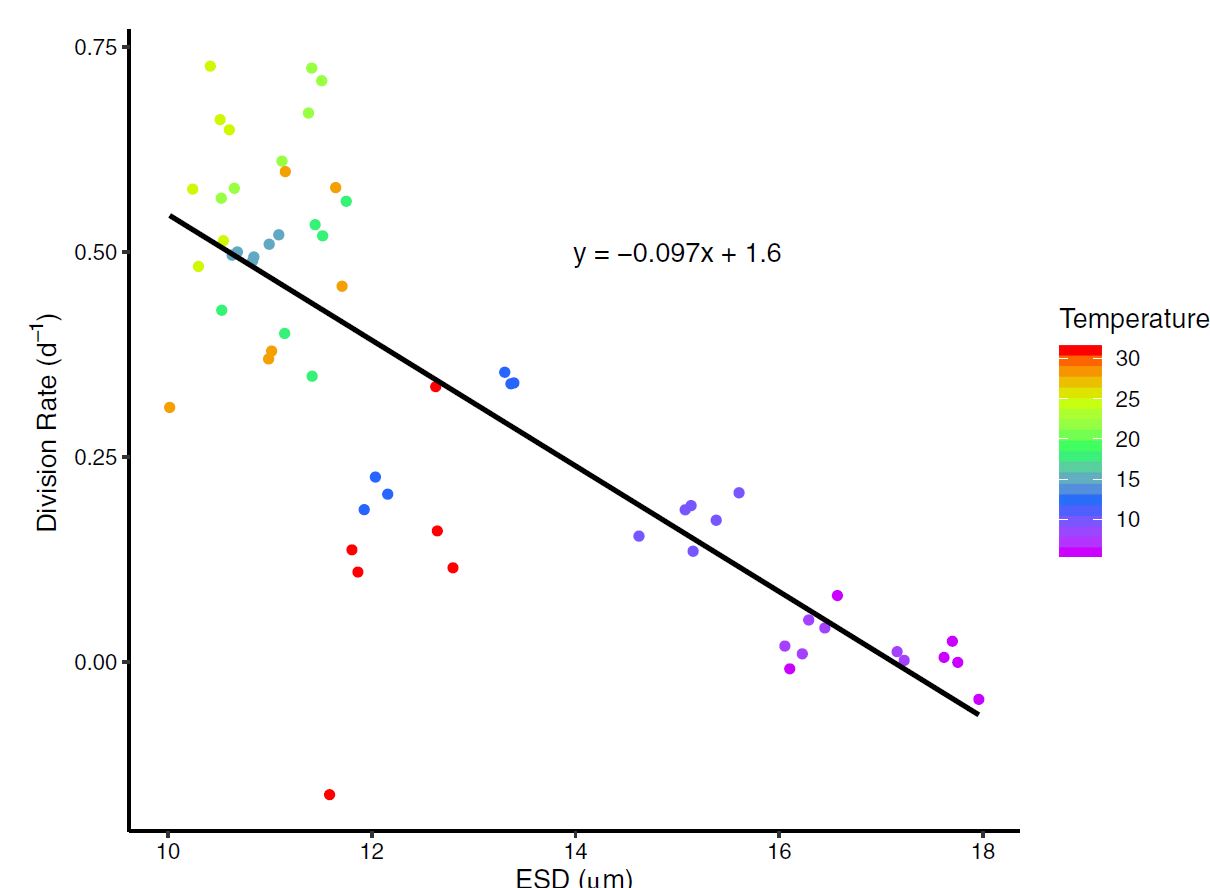Figure 5 : A type II regression fit between ESD (cell size) and division Rate (population growth rate). The temperature treatement where each measurement was recorded is shown in color.

3.) How much does change itself impact population growth and cell size?

To quantify the effect of time (acclimation) on specific growth rate, the final rates (\(\mu_f\), 7 ≤ \(\Delta\) time ≤ 15 d) were subtracted from the initial rates, measured over the first 3 d (\(\mu_0\); \(\Delta\) time ≤ 3 d) for each temperature treatment.

A break-point detection and Dunnet’s test showed three distinct response groups: 1.) Small thermal changes which lowered growth rate immediately 2.) Medium changes which accelerated growth 3.) Extreme changes which again lowered growth. To be brief, there are biological mechanisms we hypothesize which can explain these patterns, but further detailed molecular metabolic research would be needed to understand these response patterns fully. Nonetheless, we have evidence that changing temperature dramatically effects growth rates.

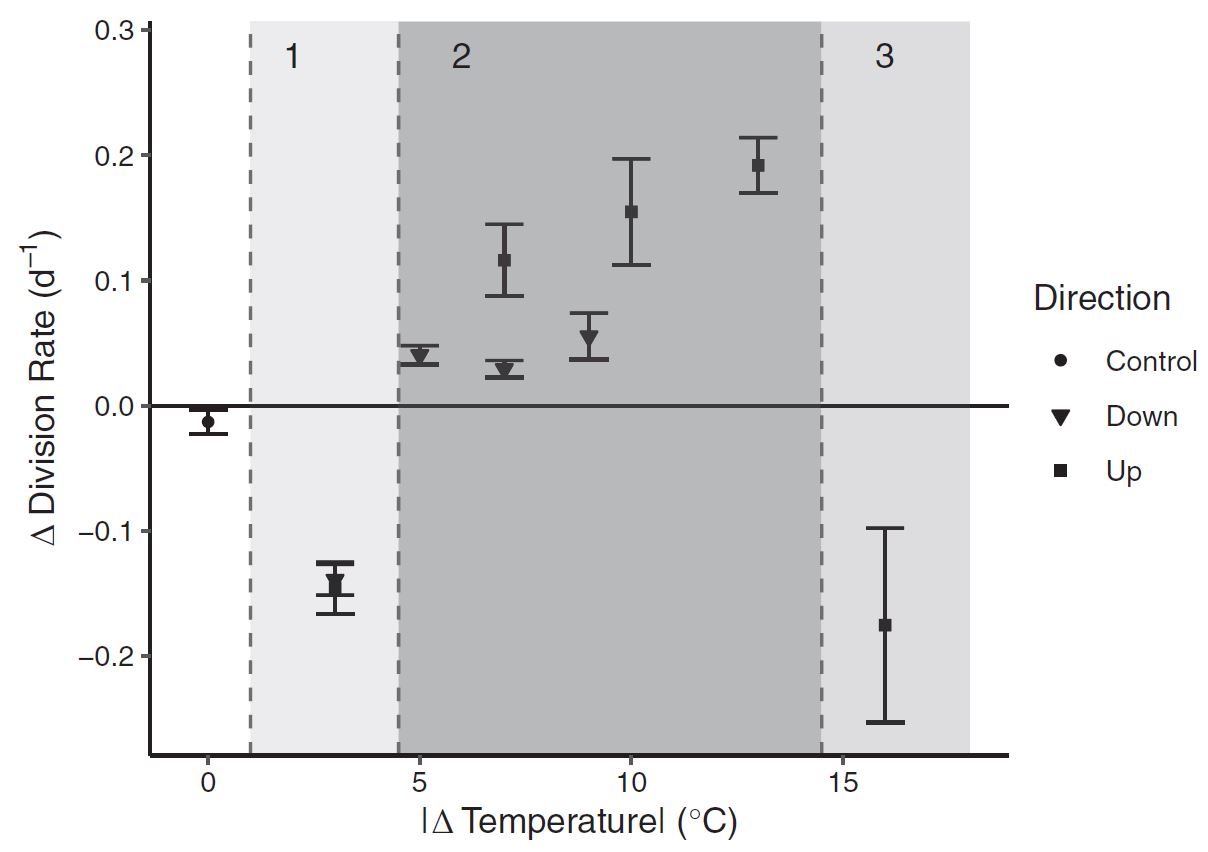Figure 6: Growth rates were dramatically impacted by the cumulative magnitude of temperature change itself.

Last, to understand patterns in the variability of growth rate among replicates as a function of the cumulative temperature change (\(\Delta\)Temperature) and time (translated into a binary variable; \(t_0\) and \(t_f\) to 0 and 1, respectively). After graphically examining the variance in growth rate relative to temperature changes, an exponential relationship was fit to the SD of the specific growth rate (σ). The following regression was again fit with maximum likelihood expectation (MLE):

where:

• c, d, and e are shape coefficients
• \(\sigma\) is the specific growth rate
• T is a given temperature
• t is the time after temperature change

Temperature change caused an exponential level increase in biological variability. And the power of the exponent decreased with time. This may seem esoteric, but the fundamental origins of biolocal variability are an open ended question in biology, and any evidence that can explain why organisms vary is valuable. Here our data evidences how environmental peturbations can rapidly diversify a population.

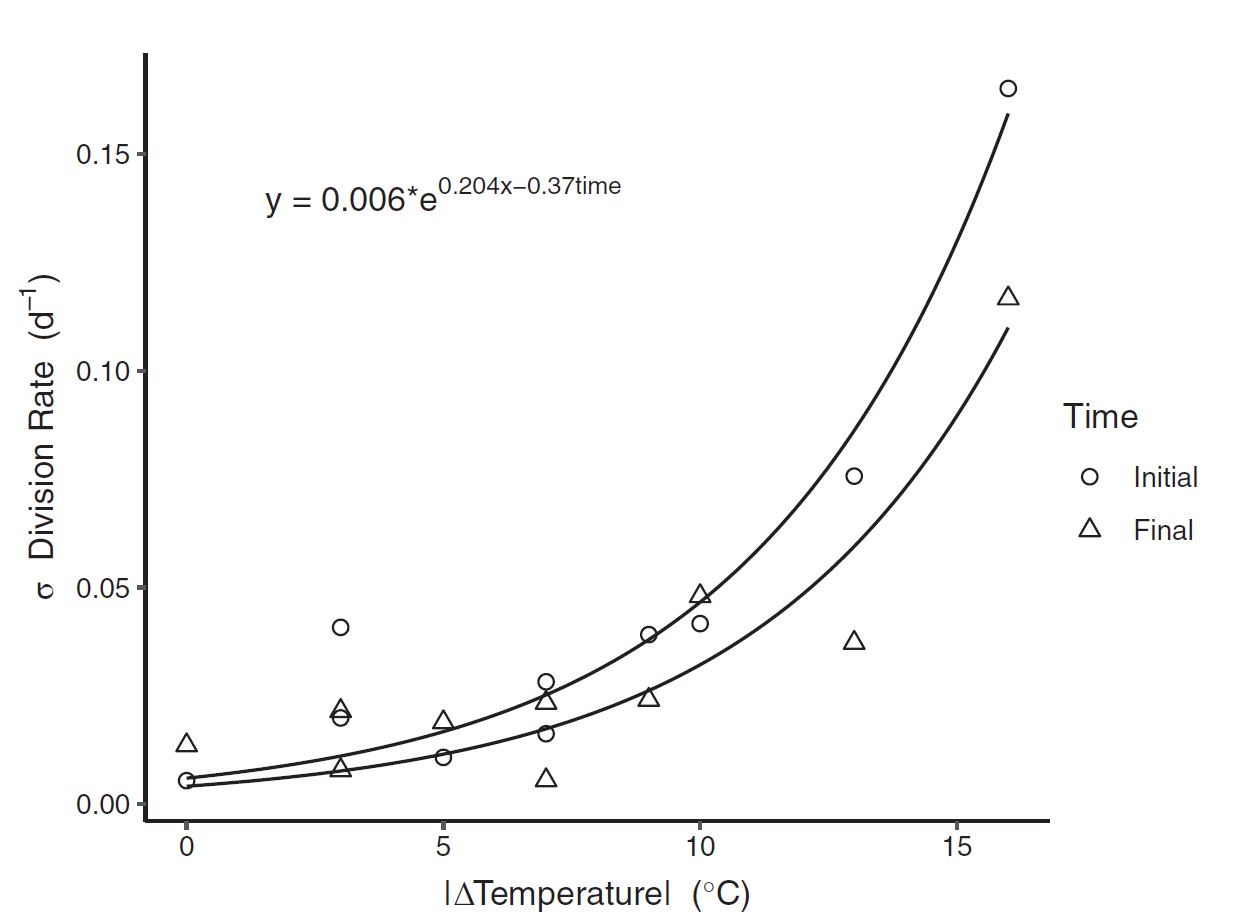Figure 7: Standard deviation in division rate (between replicates) as a function of the magnitude of temperature change. The exponential fit suggests that biological variablity increases exponentially as a result of environmental variation.

How much can thermal variability impact estimates from a standard thermal performance curve?

To exemplify, the impact of the thermal response on microbial growth as well as the potential magnitude of new-found acclimation effects, I extracted seasonal data from varied oceanographic sites within the thermal range of our study organisms. By imputting, this data into the fitted thermal performance curve we made a prediction on population growth and production.

Collecting enough laboratory data to fit any complex function or non-parameteric model to the acclimation data was impossible. As you can see from the raw data of figure 6 above, limited sample size limits the modeling options. Nevertheless, we would be remiss not to make an estimate of potential effects. Using a moving window to quantify the total temperature change an organism would experience, a scaling factor was used based on the response shown in figure 6. Consistent with the results where different magnitudes of temperature change elicited different acclimation responses, we applied a correction equal to the difference in initial and final growth rates observed at each magnitude in temperature change. Specifically, three temperature ranges in the thermal history window elicited different responses: \(3–5^{\circ}C\), \(5–13^{\circ}C\), or greater than \(13^{\circ}C\) (see “Results” section). The average specific growth rate difference (i.e., acclimation) for these three thermal ranges were −0.14 \(d^{−1}\), 0.10 \(d^{−1}\), and −0.18 \(d^{−1}\), respectively. These differences were added to the acclimated rate interpolated from the thermal performance curve. That is, when the thermal history window had a temperature range of \(3–5^{\circ}C\), \(5–13^{\circ}C\), or greater than \(13^{\circ}C\), a −0.14, 0.10, or −0.18 \(d^{−1}\) correction was added to the growth rate inferred from the thermal performance curve. Cases where no growth was observed wereomitted. The percent difference between final and initial growth responses were compared for each day.

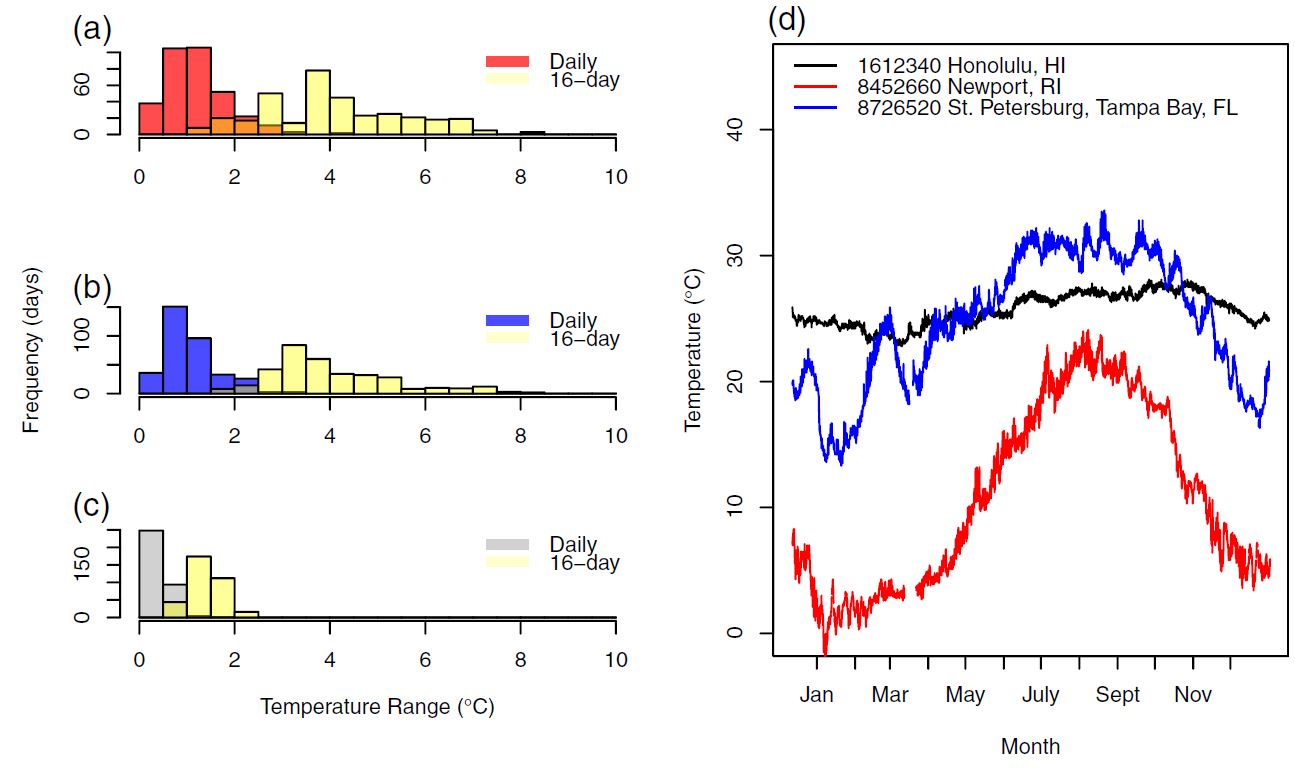Figure 7: With real-world data used for simulation, within the habitat of our target organism, temperature frequently varied to levels where we had seen measureable response to the variability itself.

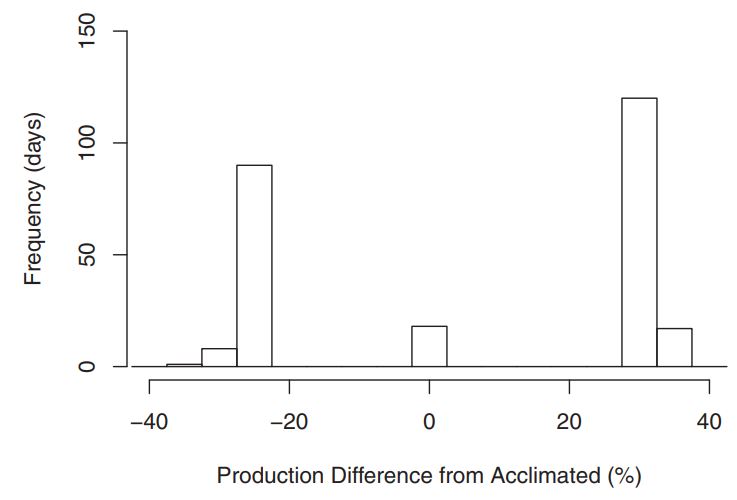Figure 8: Comparing cases to when acclimation was and wasn’t accounted for, there was potential for major discrepencies in growth estimates. The x-axis shows the magnitude of population growth differences in percent. The y-axis shows the number of days (out of 1 year) falling in each histogram bin. This results suggest that in any environment with high seasonality, further research to quantify variabilty responses will be necessary for accurate estimations.

Conclusions:

• Marine algae are highly dependent both on the magnitude of temperature, as well as thermal fluctuations
• Cell size of microbial organisms carry a clear linear relationship to division rate, and consequently may appear to vary with temperature.
• This toxic algae can handle a wide range in temperatures, and in many habitats may see continued increase in growth as the planet warms
• Biological variability intensifies exponentially as the environment changes (as seen through thermal shifts)
• Acclimation responses can impact estimates of biological production 36% under ordinary seasonal thermal conditions.

During the COVID-19 pandemic, I had the privelage to work on the Northeast Big Data Innovation Hub project CritCOVIDView: A Critical Care Visualization Tool for COVID-19. Led with the clinical and research expertise of Todd Brothers PhD, PharmD and Mohammad Al-Mamun PhD, as part of the team, I created data processing pipelines, conducted statistical analysis for insight and trained statistical models for predicting patient outcome and the clinical influences on these outcomes. The core goal of this project was to develop predictive models and statistical insights to help clinicians make data driven medical decisions during the COVID crisis with the insights and analysis from high dimensional patient data. Recently, some of the survival (aka time to event) modeling work was published in the medical journal SAGE open Medicine. In this post, I will summarize the modeling components of this paper that I worked on as part of the team.

This project targets analysis of the interaction between the prevalent and dangerous condition of Acute Kidney Injury (AKI), and the interaction with medications, patient demographics, and COVID infection.

Because of the sensitivity of the data I can neither share the data nor analysis code, but I can and will provide a description of the analysis process, results, and implications.

Objective:

Acute Kidney Injury (AKI) is a dangerous condition and unfortunately common condition in the ICU, impacting millions of patients every year and associated with a wide range in adverse patient outcomes including death. The goal of this analysis is to model the outcomes of these patients (both mortality and recovery) as well as to identify the treatment and patient conditions that may impact the patient outcome.

Data:

This study recieved all proper ethical approval (see publication details), and used deidentified, retrospective data.

226 ICU patients were included in this study. Data included all available records of vitals, demographics, medications recieved, laboratory readings (from blood-work), and oxygenation. All patient data were available in completion during the entirety of the patient stay.

Data Processing:

AKI as a condition can be classified into 3 stages (stage 3 being the most severe), and was calculated via the criteria of the Kidney Disease Improving Global Outcomes standard. To accomplish this, I created a data pipeline which used rolling windows, applied over the temporally structured data, to detect the AKI criteria during the patient staty. By applying the AKI criteria in rolling windows of the patient data, important temporal traits were retained such as the time to onset of AKI, worsening/improving of condition over time, and time between diagnose and outcome (recovery/mortality).

First, the descriptive statistics were calculated for each study group. The mean and interquantile range were calculated for each continuous variable, and for categorical variables, the count and percentage of patients meeting the conditon were calculated. To statistically test differences between the study groups, pair-wise t-tests were used for continous varaibles, and a chi-square test was used for categorical features. Fisher’s exact test was used to statistically test differences in count data for medications classes received due to the small sample sizes for patients recieiving certain medication categories.

To prepare the data for survival modeling, the data had to be processed into a time-to-event format. In this format, each row was occupied by the data for a given patient and condition status. In example, it may designate the AKI stage 1 status of patient X. If patient X was also non-AKI, a seperate row would designate their data for the non-AKI period of their stay. Each row contained an event (recovery, worsening AKI condition, mortality), the time from diagnosis or ICU entry to the event, the patient demographics, and average laboratory, oxygen, and vitals data. In addition, a dummy encoding was used for the medication classes received during their stay. Altogether, the transformed data gave information on the time to event, the event, and the patient conditions leading up to the event.

Analysis & Results:

The first basic question is how our AKI vs non-AKI patients compare. A descriptive table and pairwise comparisons (chi-square and t-test for categorical and continous variables respectively) were used to describe the differences between the cohort of AKI and non-AKI patients.

Outcomes included the time in ICU, time on mechanical ventilation, and mortality rates were also compared for each cohort

After establishing medical differences between our AKI and non-AKI patients, we then ask what might predict a patient becoming an AKI patient. AKI classification (binary reponse variable) was predicted in a LASSO logistic model, a model which penalizes parameters, such that the model can serve for feature selection. The features selected by the model provide information on what predicts AKI classification and comparison of the odds ratio between the AKI and non-AKI group inform us to the effect size.

We also asked which medication classes might influence the AKI outcome (recovery, persistence of AKI, or mortality). Because the sample size limited statistical power in survival models, I employed a fisher’s-exact test to compare the number of patients receiving a given medication class, with the patient outcome as a dependent variable. That is the test compared whether more patients with a certain outcome received a given medication category. The Fisher’s exact test was used because of the ability to statistically test small sample sizes.

I calculated the Kaplan-Meier curve, which shows survival probability by each AKI class. It is a standard in survival modeling and we chose to show it as a reference. However, usage of this curve often violates statistical assumptions, and the same is true here (Later we will go on to show with non-proportional hazard modeling how survival differences become apparent with the correct model structure). While Kaplan-Meier estimates of emperical surival probabiltiy show little difference in the survival probablity in any of the AKI groups, it does not account for competing outcomes which means, that multiple events can happen which prevent a patient from experiencing a single target event. For example, in our data, a patient may be diagnosed with AKI stage 1. The event we are monitoring may be recovery, but they may also become censored from the study because they became a more severe AKI stage, or died. Further, the often cited log-rank statistic which test for differences in survival curves by group cannot handle time-varying differences in survival probablity. Clearly, these are major assumptions that must be addressed.

As a consequence of the nature of competing hazards in our data, a cox regression was used to test the difference in the proportional hazards for recovery and mortality in each of the AKI classified patient groups and control group. The target variables in independent models were recovery and mortality. The included predictors were AKI status, demographic traits, and medication class received.

The Cox proportional hazards model, is a model for the hazard rate, or the instantaneous probability of an event occuring. Obviously, in the real world, instantaneous rates are difficult to interpret, but if this rate is integrated over time, it gives the probability of an event occuring up to that point in time. Further, the parameterization of the Cox model for the instantaneous hazard will give us valuable information about what influences the probability of an event (like recovery or mortality) occuring. The Cox proportional hazards model is configured as such:

However, analysis of the Schoenfield residuals showed significant time-variation in the covariate effects. Therefore, a non-proportional hazards model was run whereby features that signficantly time varied as indicated by Schoenfeld residuals, were given temporal flexibility.

Conclusions:

• The pairwise analysis of AKI and non-AKI patients showed that AKI patients varied significantly in many traits including vitals, laboratory results, and commorbidities

• Pairwise comparisons of outcomes showed significantly higher time in the ICU and time on mechanical ventilation for patients who were AKI classified.

• LASSO logistic regression identified the increased risk of developing AKI for patients with higher BMI, with hypo-osmolality/hypo-natremia, and on certain classes of medications, especially diuretics, anti-infectives, and gastrointestinal agents.

• The non-proportional hazards model predicting mortality showed that severe AKI patients have a mortality risk that dramatically rises over time, as compared to stage 1 and stage 2 patients who have static mortality risk. This highlights the severe danger of entering stage 3 AKI without recovering.

• The non-proportional hazards model predicting recovery showed that stage 1 AKI patients have a recovery risk that dramatically rises over time, as compared to more severe stages. This suggests that patients who develop AKI and can be kept to a low stage are likely to recover quickly. This emphasizes the importance of mitigation and reducing the potential for further kidney damage (such as by stressful medication regimes) that could worsen AKI condition and thus the potential for adverse outcomes.

Having just completed this website, I thought it would be befitting to first post what I learned about building a static website, and how it can help you in your professional journey. A personal website can be a great tool to teach others, build your network, and hey-show off some of your hard work. These are all reasons why I built this site. If you’re also in industry like me, probably most of what you do is confidential, but it can still be a good place to share techniques and open source examples.

This post will be about how to setup a free website of your own using Github pages, how to customize it as much as your heart desires with Jekyll and Ruby, and last how to add some extra flair.

Background

What is Github Pages?

Github Pages are public web pages any user can utilize that will be freely hosted on Github. Given this is Github based, you’ll need a Github account. It would also be helpful to have git on your desktop.

What is Jekyll?

Jekyll is an open source static site generator with which you can easily write content like this in basic Markdown, use HTML and CSS for structure and presentation. Jekyll does all the hard work of compiling this into HTML so you don’t have to. If you’ve ever had to write in HTML you’ll quickly learn to appreciate Jekyll.

What is Ruby?

Ruby is the programming language Jekyll is written in. If you’re doing anything ordinary you probably won’t need to write anything in Ruby, but it is helpful to know that Ruby underlies Jekyll for building the site.

Building Your Site

It is possible to build your site either with Jekyll or without. We will overview both options here:

Option 1: If you want the easiest route that gives pretty good results, you can do everything from Github without really having to think about Jekyll. To do this, the following will get you setup:

1. Add a repository with the name username.github.io
2. Under the repository, go to “Settings”
3. Under “Code & operations” go to pages
4. Choose a theme from the default templates
5. Add content to the README.md as desired
6. You can change the title and description with “title:yourtitle” and “description:yourdescription” by adding these to the _config.yml file

Voila, you have made a site under the url https://username.github.io . If you want to make additions, such as to add more pages, you can do so with Jekyll. If you are taking this option 1 route, you can see the github documentation here for additional details. Do note however, that it may take a few minutes for changes to update.

Option 2:

This second option is for those who want more control. With this, I will cover how to use custom themes, adapt them to your needs, add pages, add posts, and even getting a custom domain name for your website.

Using a custom theme and template

The amount of open source themes for Jekyll is astounding. With little effort, you can make use themes built with the design skill of professional web designers. While there are a wealth of themes of high quality, it can be a little intimidating at first to know how to update and implement them for your own needs, especially if like me you were not familiar with Jekyll and web-design before hand. Do not worry, I will take you through how to build a beautiful site with the example of the minimal mistakes theme. If you are interested in another theme, you can find a gallery of downloadable, github page compatible themes here.

There are actually several ways to implement the minimal mistakes theme, but I recommend forking the repository and using this as a template. Obviously, with your own forked version of the template, it let’s us make more changes down the line since we have access to all the code.

To build your Github page from the repository via forking, simply navigate to the minimal mistakes repository. Click the fork icon on the top right menu like such:

As in option 1, we need to rename this repository on our own profile with name username.github.io. Under the forked repository, you can do this simply by clicking on settings on the menu bar, and typing the new name of your repository in the top box:

Under “Code & operations” go to pages. Your github site should now be up and running on https://username.github.io.

Of course, what you see are all the default pages and content for this theme. How do we include our information and customize?

Building and Serving Locally

Because we are really starting with a blank template of a site, and you are going to want to visualize your changes as you go, it is best to add your content locally. In essence, adding everything is possible directly from your profile it Github but it will be particularly painful because commits will take several minutes to take effect.

For your local environment, you will need git installed and ssh-key properly setup. You will also need Jekyll and Ruby. For installation and setup, I will point you to an excellent tutorial for both Windows and Mac. Last, you will need a text editor, I recommend Visual Studio Code, because it facilitates fast staging, commits, and push to your Github. This means you’ll be able to develop quickly and easily. Lets get started.

First, clone your Github repo locally. You can do this from Git Bash via _git clone _. You now have all the template files locally on your computer where you can edit them.

From your command line, navigate to your cloned repo and enter bundle exec jekyll serve. This will serve the site locally on your PC. It should default to localhost:4000, which you can type in any browser. Changes to posts and pages will take place immediately, but config changes will require quitting and restarting the serve command. Nevertheless, this will let you start making additions and changes to your site while seeing how they impact the webpage.

With your PC serving your site locally, go ahead and navigate to your repository folder in VS code. There are several major folders and files to adapt the site to your needs:

1. _ config.yml : Includes most of the site-wide configuration, and home page attributes. If you are working from a template, this should be pretty straight forward to adapt to your use. Just replace
2. _ posts: Includes markdown files each with an individual post
3. _ pages: Includes markdown files for separate pages on the site
4. _ data: Includes important reference data across the site such as dictionary of page names and associated URL
5. _ assets: A place you can put documents and images to link and embed in your text

Custom domain name

So far so good. But if you’re like me you might be bothered by having to stick with the standard domain name for your site. If you want to get creative or maybe just don’t want to have .github.io in the address, not to fear, Github has made this easy.

If you don’t already own a domain name, this is pretty simple. There are a number of domain name services. I chose GoDaddy.com, but it doesn’t matter which you use.

Once you buy a domain name, you’ll have to make a few changes with your domain managment and Github to get it working, but it’s a sinch.

On the DNS management page, you need to make the following changes:

1. For variable “A”, update the IP address to: 185.199.108.153 to point your domain to Github’s server over HTTPS
2. Add three for variable “A” with the following IP addresses: 185.199.109.153, 185.199.110.153, 185.199.111.153
3. In CNAME input your current Github pages site username.github.io

In the Github repository for your site, add a file “CNAME” in the root directory. In CNAME, add your purchased domain name.